Difference in contact potential

If two samples made of two different metals are tightly pressed together, then a contact potential difference will occur between them. Italian physicist, chemist and physiologist Alessandro Volta discovered this phenomenon in 1797 while studying the electrical properties of metals.

Then Volta found that if you connect the metals in a chain in this order: Al, Zn, Sn, Pb, Bi, Hg, Fe, Cu, Ag, Au, Pt, Pd, then each subsequent metal in the resulting chain will acquire a potential of - lower than the previous one. Moreover, the scientist found that several metals combined in this way will give the same potential difference between the ends of the circuit formed, regardless of the sequence of arrangement of these metals in this circuit - this position is now known as Volta's law of series contacts .

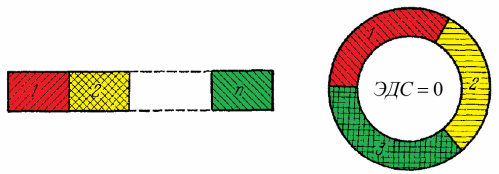
Here it is extremely important to understand that for the exact implementation of the law of contact sequence, it is necessary that the entire metal circuit be at the same temperature.

If this circuit is now closed from the ends on itself, then it follows from the law that the EMF in the circuit will be zero.But only if all of these (metal 1, metal 2, metal 3) are at the same temperature, otherwise the basic law of nature—the law of conservation of energy—would be violated.

For different pairs of metals, the contact potential difference will be its own, ranging from tenths and hundredths of a volt to a few volts.

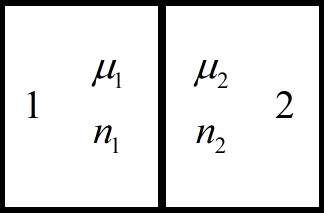
To understand the reason for the appearance of the contact potential difference, it is convenient to use the free electron model.

Let both metals of the pair be at absolute zero temperature, then all energy levels, including the Fermi limit, will be filled with electrons. The value of the Fermi energy (limit) is related to the concentration of conduction electrons in the metal as follows:

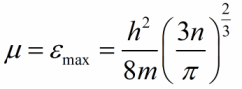
m is the rest mass of the electron, h is Planck's constant, n is the concentration of conduction electrons

Taking this ratio into account, we bring into close contact two metals with different Fermi energies and therefore with different concentrations of conduction electrons.

Let us assume for our example that the second metal has a high concentration of conduction electrons and accordingly the Fermi level of the second metal is higher than that of the first.

Then, when the metals come into contact with each other, a diffusion (penetration from one metal to another) of electrons will begin from metal 2 to metal 1, because metal 2 has filled energy levels that are above the Fermi level of the first metal , which means that electrons from these levels will fill in metal 1 vacancies.

The reverse movement of electrons in such a situation is energetically impossible, since in the second metal all the lower energy levels are already completely filled.Eventually, metal 2 will become positively charged and metal 1 negatively charged, while the Fermi level of the first metal will become higher than it was, and that of the second metal will decrease. This change will be as follows:

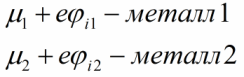
As a result, a potential difference will arise between the contacting metals and the corresponding electric field, which will now prevent further diffusion of electrons.

Its process will stop completely when the potential difference reaches a certain value corresponding to the equality of the Fermi levels of the two metals, at which there will be no free levels in metal 1 for the newly arrived electrons from metal 2, and in metal 2 no levels will be freed on the possibility of electron migration from metal 1. The energy balance will come:

Since the charge of the electron is negative, we will have the following position relative to the potentials:

Although we have originally assumed the temperature of the metals to be absolute zero, yet in a similar manner equilibrium will occur at any temperature.

The Fermi energy in the presence of an electric field will be nothing more than the chemical potential of a single electron in an electron gas referred to the charge of that single electron, and since under equilibrium conditions the chemical potentials of the electron gases of both metals will be equal , it is only necessary to add to the consideration the dependence of the chemical potential on temperature.

So, the potential difference considered by us is called the internal contact potential difference and corresponds to Volta's law for series contacts.

Let's estimate this potential difference, for this we express the Fermi energy in terms of the concentration of conduction electrons, then substitute the numerical values ​​of constants:

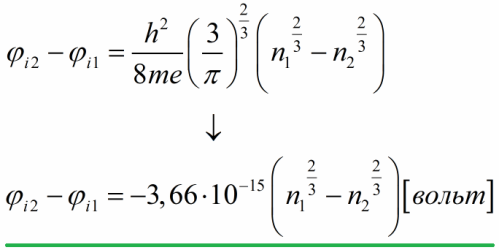
Thus, based on the free electron model, the internal contact potential difference for metals is on the order of magnitude from hundredths of a volt to several volts.