Electrocapillary phenomena

If the surface of the electrolyte is charged, then the surface tension on its surface depends not only on the chemical composition of the neighboring phases, but also on their electrical properties. These properties are the surface charge density and the potential difference at the interface.

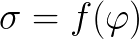
The dependence (e) of the surface tension on the potential difference for this phenomenon is described by an electrocapillary curve. And the very surface phenomena where this dependence is observed are called electrocapillary phenomena.

Allow the electrode potential to change in some way at the electrode-electrolyte interface. In this case, there are ions on the metal surface that form a surface charge and cause the presence of an electric double layer, although there is no external EMF here at all.

Like-charged ions repel each other across the surface of the interface, thus compensating for the contractile forces of the liquid molecules. As a result, the surface tension becomes lower than in the absence of an excess potential on the electrode.

If a charge of the opposite sign is applied to the electrode, the surface tension will increase because the forces of mutual repulsion of ions will decrease.

In the case of absolute compensation of the attractive forces by the electrostatic forces of the repulsive ions, the surface tension reaches a maximum. If we continue to supply the charge, then the surface tension will decrease as new surface charge will arise and grow.

In some cases, the importance of electrocapillary phenomena is very great. They make it possible to change the surface tension of liquids and solids, as well as to influence colloidal-chemical processes such as adhesion, wetting and dispersion.

Let us turn our attention again to the qualitative side of this dependence. Thermodynamically, surface tension is defined as the work of the isothermal process of forming a unit surface.

When there are electric charges of the same name on a surface, they will electrostatically repel each other. The forces of electrostatic repulsion will be directed tangentially to the surface, trying to increase its area anyway. As a result, the work to stretch the charged surface will be less than the work that would be required to stretch a similar but electrically neutral surface.

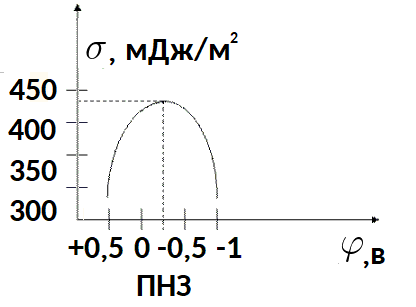
As an example, let us take the electrocapillary curve for mercury in aqueous solutions of electrolytes at room temperature.

At the point of maximum surface tension the charge is zero. The mercury surface is electrically neutral under these conditions.Thus, the potential at which the electrode surface tension is maximum is the zero charge potential (ZCP).

The magnitude of the potential of zero charge is related to the nature of the liquid electrolyte and the chemical composition of the solution. The left side of the electrocapillary curve, where the surface potential is less than the potential of zero charge, is called the anodic branch. The right side is the cathode branch.

It should be noted that very small changes in potential (on the order of 0.1 V) can produce noticeable changes in surface tension (on the order of 10 mJ per square meter).

The dependence of the surface tension on the potential is described by the Lippmann equation:

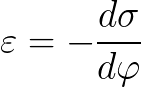
Electrocapillary phenomena find practical application in the application of various coatings on metals — they make it possible to regulate the wetting of solid metals with liquids. The Lippmann equation allows calculation of the surface charge and capacitance of the electric double layer.

With the help of electrocapillary phenomena, the surface activity of surfactants is determined, since their ions have a specific adsorption. In molten metals (zinc, aluminum, cadmium, gallium) their adsorption capacity is determined.

The electrocapillary theory explains the maxima in polarography. The dependence of the wettability, hardness and coefficient of friction of the electrode on its potential also refers to electrocapillary phenomena.