Electrical capacity of the cable

When switching DC voltage on or off in a cable network or under the influence of AC voltage, a capacitive current always occurs. Long-term capacitive current exists only in the insulation of cables under the influence of alternating voltage. Constant current conduction exists at all times and a constant current is applied to the cable insulation. In more detail about the capacity of the cable, about the physical meaning of this characteristic and will be discussed in this article.

From the point of view of physics, a solid circular cable is essentially a cylindrical capacitor. And if we take the value of the charge of the inner cylindrical plate as Q, then per unit of its surface there will be an amount of electricity that can be calculated by the formula:

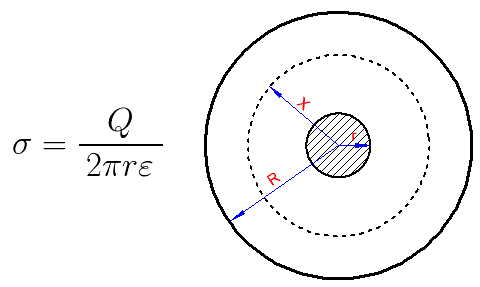
Here e is the dielectric constant of the cable insulation.

According to fundamental electrostatics, the electric field strength E at radius r will be equal to:

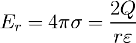
And if we consider the inner cylindrical surface of the cable at some distance from its center, and this will be the equipotential surface, then the electric field strength per unit area of ​​this surface will be equal to:

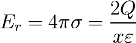
The dielectric constant of cable insulation varies widely depending on operating conditions and the type of insulation used. Thus, vulcanized rubber has a dielectric constant of 4 to 7.5, and impregnated cable paper has a dielectric constant of 3 to 4.5. Below it will be shown how the dielectric constant, and hence the capacitance, are related to temperature.

Let's turn to Kelvin's mirror method. Experimental data only give formulas for approximate calculation of cable capacitance values, and these formulas are obtained based on the specular reflection method. The method is based on the position that a cylindrical metal shell surrounding an infinitely long thin wire L charged to a value Q affects this wire in the same way as a wire L1 oppositely charged, but provided that:

Direct capacitance measurements give different results with different measurement methods. For this reason, cable capacity can be roughly divided into:

• Cst — static capacitance, which is obtained by continuous current measurement with subsequent comparison;

• Seff is the effective capacitance, which is calculated from the voltmeter and ammeter data when testing with alternating current by the formula: Сeff = Ieff /(ωUeff)

• C is the actual capacitance, which is obtained from the analysis of the oscillogram in terms of the ratio of the maximum charge to the maximum voltage during the test.

In fact, it turned out that the value of C of the actual capacitance of the cable is practically constant, except in cases of insulation breakdown, therefore the change in voltage does not affect the dielectric constant of the insulation of the cable.

However, the influence of temperature on the dielectric constant is realized and with increasing temperature it decreases to 5% and accordingly the actual capacitance C of the cable decreases. In this case, there is no dependence of the actual capacity on the frequency and shape of the current.

The static capacity Cst of the cable at temperatures below 40 ° C is consistent with the value of its actual capacity C and this is due to the dilution of the impregnation; at higher temperatures, the static capacity Cst increases. The nature of the growth is shown in the graph, curve 3 on it shows the change in the static capacity of the cable with a change in temperature.

The effective capacitance Ceff is strongly dependent on the current shape. A pure sinusoidal current results in a coincidence of effective and real capacitance. A sharp current form leads to an increase in the effective capacity by one and a half times, a blunt current form reduces the effective capacity.

The effective capacity Ceff is of practical importance, as it determines the important characteristics of the electrical network. With ionization in the cable, the effective capacitance increases.

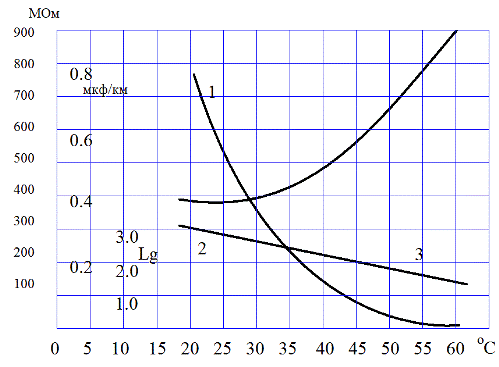
In the graph below:

1 — dependence of cable insulation resistance on temperature;

2 — logarithm of cable insulation resistance versus temperature;

3 — dependence of the value of the static capacity Cst of the cable on the temperature.

During the production quality control of the cable insulation, the capacity is practically not decisive, except in the process of vacuum impregnation in a drying boiler. For low-voltage networks, capacitance is also not very important, but it affects the power factor with inductive loads.

And when working in high-voltage networks, the capacity of the cable is extremely important and can cause problems during the operation of the installation as a whole. For example, you can compare installations with an operating voltage of 20,000 volts and 50,000 volts.

Let's say you need to transmit 10 MVA with a cosine of phi equal to 0.9 for a distance of 15.5 km and 35.6 km. For the first case, the cross-section of the wire, taking into account the permissible heating, we choose 185 sq. Mm, for the second - 70 sq. Mm. The first 132 kV industrial installation in the USA with an oil-filled cable had the following parameters: the charging current of 11.3 A / km gives a charging power of 1490 kVA / km, which is 25 times higher than the analogous parameters of the overhead transmission lines of similar voltage.

In terms of capacity, the Chicago underground installation in the first stage proved to be similar to a parallel-connected electrical capacitor of 14 MVA, and in New York City the capacitive current capacity reached 28 MVA and this with a transmitted power of 98 MVA. The working capacity of the cable is approximately 0.27 Farads per kilometer.

No-load losses when the load is light are caused precisely by the capacitive current, which generates Joule heat, and full load contributes to the more efficient operation of power plants. In an unloaded network, such a reactive current lowers the voltage of the generators, which is why special requirements are imposed on their designs.In order to reduce the capacitive current, the frequency of the high-voltage current is increased, for example, during cable testing, but this is difficult to implement, and sometimes resorting to charging the cables with inductive reactors.

So the cable always has capacitance and ground resistance which determine the capacitive current. The insulation resistance of the cable R at a supply voltage of 380 V must be at least 0.4 MΩ. The capacity of cable C depends on the length of the cable, the way of laying, etc.

For a three-phase cable with vinyl insulation, voltage up to 600 V and network frequency 50 Hz, the dependence of the capacitive current on the cross-sectional area of ​​the current-carrying wires and its length is shown in figure. Data from the cable manufacturer's specifications should be used to calculate the capacitive current.

If the capacitive current is 1 mA or less, it does not affect the operation of the drives.

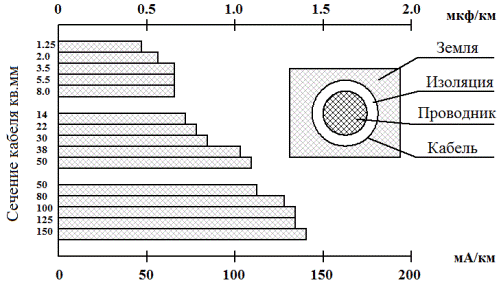
The capacity of cables in grounded networks plays an important role. Grounding currents are almost directly proportional to capacitive currents and, accordingly, to the capacitance of the cable itself. Therefore, in large metropolitan areas, the ground currents of huge urban networks reach enormous values.

We hope that this short material has helped you to get a general idea about cable capacity, how it affects the operation of electrical networks and installations, and why it is necessary to pay due attention to this cable parameter.