Fundamentals and Laws of the Algebra of Logic

Irish mathematician of the mid-19th century George Bull developed the algebra of logic ("Study of the laws of thinking"). Hence the algebra of logic is also called boolean algebra.

By giving letter designations, expressing the operations of logical transformations in action symbols, and using the rules and axioms established for these actions, the algebra of logic allows the reasoning process in solving a problem given in terms of statement logic to be fully described in algorithms, that is, to have a mathematically written program solving this problem.

To denote the truth or falsity of statements (that is, to introduce values ​​for evaluating statements), the algebra of logic uses a binary system, convenient in this case. If the statement is true, it takes the value 1, if it is false, it takes the value 0. Unlike binary numbers, logical 1s and 0s do not express a quantity, but a state.

So, in electrical circuits described using Boolean algebra, where 1 is the presence of voltage and 0 is its absence, the supply of voltages from several sources to one node of the circuit (that is, the arrival of several logical units of it) is also shows as a logical unit that indicates not the total voltage at the node, but only its presence.

When describing the input and output signals of the logic circuits, variables are used that take the values ​​of only logical 0 or 1. The dependence of the output signals on the input is determined logical operation (function)… Let us denote the input variables by X1 and X2, and the output obtained by a logical operation on them by y.

Think it over three basic elementary logical operations, with the help of which increasingly complex ones can be described.

1. OR operation — logical addition:

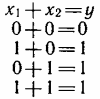
Given all the possible values ​​of the variables, one can define the OR operation as the sufficiency of at least one unit in the input to produce one in the output. The name of the operation is explained by the semantic meaning of the union OR in the phrase: «If OR is one input OR the second is one, then the output is one.»

2. Operation AND — logical multiplication:

From considering the full set of values ​​of the variables, the AND operation is defined as the need to match all the ones on the inputs to get a one on the output: “If AND is one input and the second is ones, then the output is one. «

3. Operation NOT — logical negation or inversion. It is indicated by a bar above the variable.

When reversed, the value of the variable is reversed.

Basic laws of logical algebra:

1. The Law of the Zero Set: the product of any number of variables vanishes if any of the variables is zero, regardless of the values ​​of other variables:

2. The law of the universal set — the sum of any number of variables becomes one if at least one of the variables has the value one, regardless of other variables:

3. The Law of Repetition — repeated variables in the expression can be omitted (in other words, there is no exponentiation and multiplication by a numerical coefficient in Boolean algebra):

4. The law of double inversion — the inversion performed twice is an empty operation:

5. Law of complementarity — the product of each variable and its inverse is zero:

6. The sum of each variable and its reciprocal is one:

7. Protective Laws — the result of performing multiplication and addition operations does not depend on the order in which the variables follow:

8. Combined Laws — during multiplication and addition operations, variables can be grouped in any order:

9. Distribution Laws — it is allowed to put the total coefficient outside the brackets:

10. Laws of absorption — indicate ways to simplify expressions involving a variable in all factors and terms:

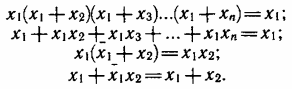
11. De Morgan's laws — the inversion of the product is the sum of the inversions of the variables:

the inversion of the sum is the product of the inversions of the variables: