The action of a magnetic field on a current-carrying conductor

If we try to put two identical permanent ring magnets together with opposite poles, then at some point when they get closer, they will start to attract more and more to each other.

And if you try to bring the same magnets closer together, but with the poles of the same name, then at a certain distance they will increasingly hinder this convergence, they will try to spread to the sides, as if they repel each other.

This means that near the magnets there is some immaterial matter that exhibits these properties, exerts a mechanical effect on the magnets, and the strength of this effect is not the same at different distances from the magnets, the closer it is, the stronger it is .This intangible matter is called magnetic field.

Science has long known that the source of a magnetic field is an electric current. In permanent magnets, these microcurrents are inside molecules and atoms, but there are many, many many such currents, and the total magnetic field is the magnetic field permanent magnet.

If we take a separate current-carrying wire, then it also has a magnetic field.And this magnetic field is able to interact with other magnetic fields in the same way. That is, a current-carrying conductor interacts with an external magnetic field.

The law of the interaction of a conductor with a current and a magnetic field was established by a French physicist Andre-Marie Ampere in the first half of the 19th century.

Ampere experimentally showed that a current-carrying conductor in a magnetic field is affected by a force whose direction and magnitude depend on the magnitudes and relative position of the current and the magnetic induction vector of the magnetic field in which the current conductor is located. This force is called today Ampere strength… Here is his formula:

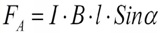
Here:

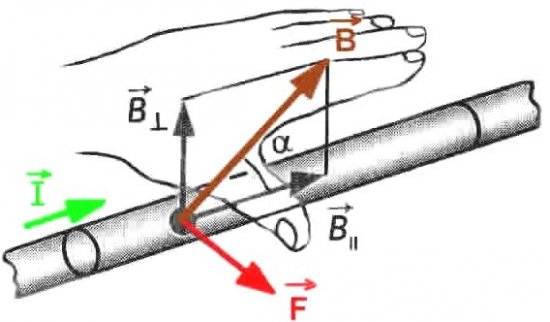
a is the angle between the current direction and the magnetic induction vector;

B — magnetic induction of the external magnetic field at the location of the current-carrying conductor;

I is the amount of current in the wire;

l is the active length of the current-carrying wire.

The magnitude of the force acting on the side of the magnetic field on the current-carrying conductor is numerically equal to the product of the modulus of the magnetic induction of the length of the conductor element placed in the magnetic field and the magnitude of the current in the conductor, and is also proportional to the sine of the angle between the direction of the current and the direction of the magnetic induction vector.

The direction of Ampere's force is determined according to the left-hand rule: if the left hand is positioned so that the perpendicular component of the magnetic induction vector B enters the palm, and four outstretched fingers are directed in the direction of the current, then the thumb, bent at 90 degrees, will indicate the direction of the force acting on a segment of current-carrying wire, that is, the direction of the Ampere force.

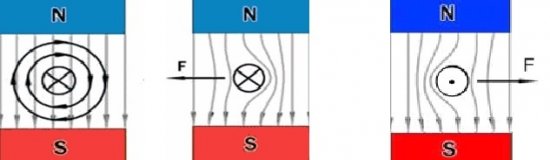
Since the magnetic field obeys the principle of superposition of fields, the magnetic field of the current-carrying conductor and the magnetic field in which that conductor is located add up in the space around the conductor.

As a result, the picture of the interaction of the current with the magnetic field looks as if the wire is pushed from the region where the magnetic field is more concentrated to the region where the magnetic field is less concentrated.

The region where the magnetic field is stronger can be imagined as filled with tightly stretched filaments, which tend to push the conductor in the direction where the filaments are weaker.