Electrons behave like waves

Physicists have long known that light is an electromagnetic wave. To this day, no one doubts this position, since light clearly demonstrates all the signs of wave behavior: light waves can overlap each other, generating an interference pattern, they are also able to separate, bending around obstacles along diffraction time.

When we see a bird that walks like a duck, swims like a duck, and quacks like a duck, we call that bird a duck. So the light is electromagnetic wavebased on objectively observed signs of the behavior of such a wave in light.

However, in the late 19th and 20th centuries, physicists were to start talking about the «particle-wave dualism» of light. It turns out that the knowledge that light is an electromagnetic wave is not all that science knows about light. Scientists have discovered a very interesting feature in light.

It turns out that somehow light manifests itself AS the behavior of a stream of particles somehow.It was found that the energy carried by the light, after being counted over a certain period of time by a special detector, turns out to be composed anyway of individual (whole) pieces.

Therefore, it became true that the energy of light is discrete, because it is composed, as it were, of individual particles - "quanta", that is, of the smallest whole portions of energy. Such a particle of light, carrying a unit (or quantum) of energy, came to be called a photon.

The energy of one photon is found by the following formula:

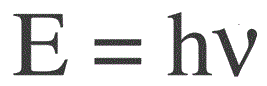
E — photon energy, h — Planck's constant, v — frequency.

The German physicist Max Planck first experimentally established the fact of the discreteness of the light wave and calculated the value of the constant h, which appears in the formula for finding the energy of individual photons. This value turned out to be: 6.626 * 10-34 J * s. Planck published the results of his work in the late 1900s.

Consider, for example, a purple ray. The frequency of such light (f or v) is 7.5 * 1014 Hz Planck's constant (h) is 6.626 * 10-34 J * s. This means that the energy of the photon, (E), characteristic of the color violet, is 5 * 10-19 J. This is such a small portion of energy that it is very difficult to capture.

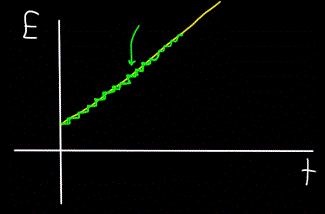
Imagine a mountain stream — it flows as one unit, and it is impossible to see with the naked eye that the stream is actually made up of individual water molecules. Today, however, we know that the macroscopic object—flow—is actually discrete, that is, it consists of individual molecules.

This means that if we can place a molecule counter next to the stream to count the water molecules passing by as the stream flows, the detector will always only count whole numbers of water molecules, not partial ones.

Similarly, the graph of the total energy of the photon E, calculated at time t — will always turn out to be not linear (yellow figure), but stepwise (green figure):

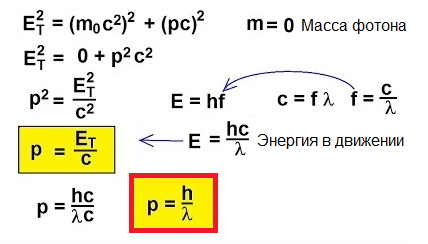
So, photons move, they carry energy, therefore they have momentum. But a photon has no mass. How then can you find momentum?

In fact, for objects moving at speeds close to the speed of light, the classical formula p = mv is simply inapplicable. To understand how to find momentum in this unusual case, let's turn to special relativity:

In 1905, Albert Einstein explained from this point of view photoelectric effect… We know that the metal plate has electrons within it, which inside it are attracted by the positively charged nuclei of the atoms and are therefore retained in the metal. But if you shine such a plate with light of a CERTAIN frequency, then you can knock electrons out of the plate.

It's as if light behaves like a stream of particles with momentum. And even though a photon has no mass, it still somehow interacts with an electron in a metal, and under certain conditions a photon is able to knock out an electron.

So if a photon incident on the plate has enough energy, then the electron will be knocked out of the metal and move out of the plate with velocity v. Such a knocked out electron is called a photoelectron.

Since the knocked out electron has a known mass m, it will have a certain kinetic energy mv.

The energy of the photon, when it acted on the metal, is converted into the energy of the exit of the electron from the metal (work function) and into the kinetic energy of the electron, possessing which the knocked-out electron begins to move out of the metal, leaving it.

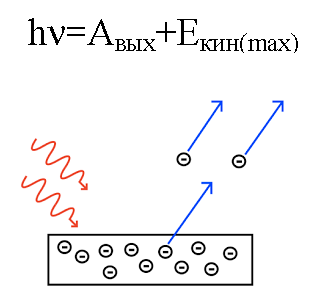
Suppose a photon of known wavelength strikes the surface of a metal for which the work function (of an electron from the metal) is known. In this case, the kinetic energy of an electron emitted from a given metal can easily be found, as well as its velocity.

If the energy of the photon is not sufficient for the electron to perform the work function, then the electron simply cannot leave the surface of the given metal and the photoelectron is not formed.

In 1924, a French physicist Louis de Broglie put forward a breakthrough idea according to which not only photons of light but electrons themselves can behave like waves. The scientist even derived a formula for the hypothetical wavelength of the electron. These waves were subsequently called "de Broglie waves".

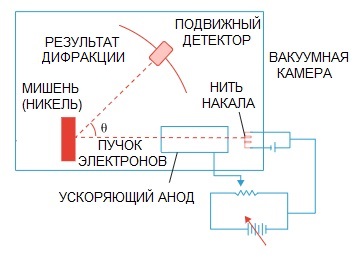
De Broglie's hypothesis was later confirmed. A physics experiment on electron diffraction, conducted in 1927 by American scientists Clinton Davison and Lester Germer, finally pointed out the wave nature of the electron.

When a beam of electrons was directed through a special atomic structure, it seems that the detector should have recorded the picture as particles flying one after the other, which would logically be expected if electrons were particles.

But in practice we have a picture characteristic of wave diffraction. Moreover, the lengths of these waves are completely consistent with the concept proposed by de Broglie.

Ultimately, de Broglie's idea made it possible to explain the principle of Bohr's atomic model, and later it made it possible for Erwin Schrödinger to generalize these ideas and lay the foundations of modern quantum physics.