Interaction of parallel conductors with current (parallel currents)

At some point in space, the induction vector of the magnetic field B generated by a direct electric current I can be determined using the Biot-Savard law… This is done by summing all the contributions to the magnetic field from the individual current cells.

The magnetic field of the current element dI, at the point defined by the vector r, according to the Biot-Savart law is found as follows (in the SI system):

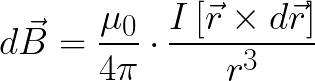
One of the typical tasks is to further determine the interaction strength of the two parallel currents. After all, as you know, currents generate their own magnetic fields, and a current in a magnetic field (of another current) experiences Amperage action.

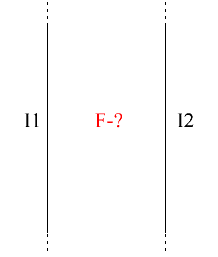
Under the action of Ampere's force, oppositely directed currents repel each other, and currents directed in the same direction attract each other.

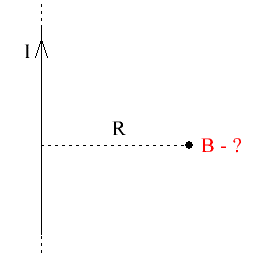
First of all, for direct current I, we need to find the magnetic field B at some distance R from it.

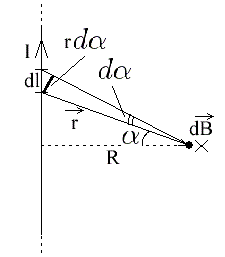
For this, an element of current length dl (in the direction of the current) is introduced and the contribution of the current at the location of this element of length to the total magnetic induction relative to the selected point in space is taken into account.

First we will write expressions in the CGS system, that is, the coefficient 1 / s will appear, and at the end we will give the record in NEwhere the magnetic constant appears.

According to the rule for finding the cross product, the vector dB is the result of the cross product dl of r for each element dl, regardless of where it is located in the considered conductor, it will always be directed outside the plane of the drawing. The result will be:

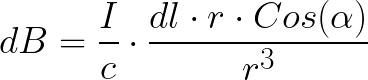
The product of the cosine and dl can be expressed in terms of r and the angle:

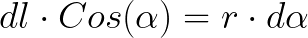
So the expression for dB will take the form:

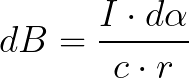
Then we express r in terms of R and the cosine of the angle:

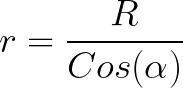
And the expression for dB will take the form:

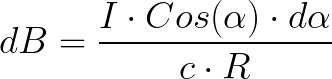
Then it is necessary to integrate this expression in the range from -pi / 2 to + pi / 2 and as a result we obtain for B at a point at a distance R from the current the following expression:

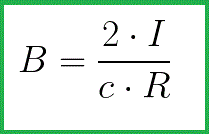
We can say that the vector B of the found value, for the selected circle of radius R, through the center of which a given current I passes perpendicularly, will always be directed tangentially to this circle, no matter which point of the circle we choose. There is axial symmetry here, so the vector B at every point on the circle is the same length.

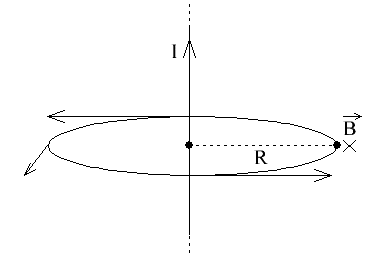
Now we will consider parallel direct currents and solve the problem of finding the forces of their interaction. Assume that the parallel currents are directed in the same direction.

Let us draw a magnetic field line in the form of a circle of radius R (which was discussed above).And let the second conductor be placed parallel to the first at some point on this field line, that is, at a place of induction, the value of which (depending on R) we have just learned to find.

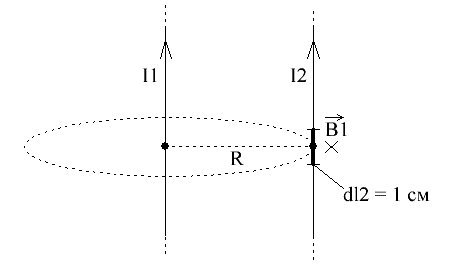
The magnetic field at this location is directed beyond the plane of the drawing and acts on the current I2. Let's choose an element with current length l2 equal to one centimeter (a unit of length in the CGS system). Then consider the forces acting on it. We will use Ampere's Law… We found the induction at the site of the element of length dl2 of the current I2 above, it is equal to:

Therefore, the force acting from the entire current I1 per unit length of current I2 will be equal to:

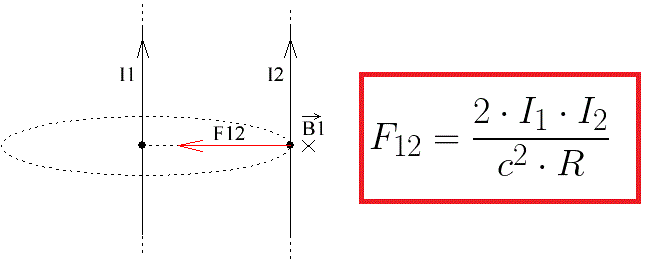
This is the force of interaction of two parallel currents. Since the currents are unidirectional and they attract, the force F12 on the side of the current I1 is directed so as to pull the current I2 towards the current I1. On the side of the current I2 per unit length of the current I1 there is a force F21 of equal magnitude but directed in the direction opposite to the force F12, in accordance with Newton's third law.

In the SI system, the interaction force of two direct parallel currents is found by the following formula, where the proportionality factor includes the magnetic constant: