Flow and circulation of a vector field

NBased on Richard Feynman's lecture materials

When describing the laws of electricity in terms of vector fields, we are faced with two mathematically important features of the vector field: flux and circulation. It would be nice to understand what these mathematical concepts are and what their practical meaning is.

The second part of the question is easy to answer right away because the concepts of flow and circulation are at the heart of Maxwell's equations, on which all modern electrodynamics actually rests.

So, for example, the law of electromagnetic induction can be formulated as follows: the circulation of the electric field E along a closed loop C is equal to the rate of change of the flux of the magnetic field B through the surface S bounded by this loop B.

In what follows, we will describe quite simply, using clear fluid examples, how the field characteristics are mathematically determined, from which these field characteristics are taken and obtained.

Vector field flux

To begin with, let us draw a certain closed surface of completely arbitrary shape around the area under study. After depicting this surface, we ask whether the object of study, which we call a field, flows through this closed surface. To understand what this is all about, consider a simple liquid example.

Let's say we are investigating the velocity field of a certain fluid. For such an example, it makes sense to ask: does more fluid pass through this surface per unit time than flows into the volume bounded by this surface? In other words, is the outflow rate always directed primarily from the inside out?

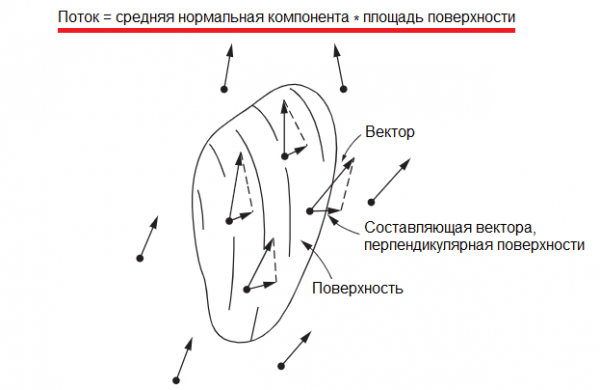
By the expression "vector field flux" (and for our example the expression "fluid velocity flux" will be more accurate), we will agree to name the total amount of imaginary fluid that flows through the surface of the considered volume bounded by given a closed surface (for the fluid flow rate, how much fluid follows from the volume per unit time).

As a result, the flux through the surface element will be equal to the product of the area of ​​the surface element by the perpendicular component of the velocity. Then the total (total) flux across the entire surface will be equal to the product of the average normal component of the velocity, which we will count from the inside out, by the total surface area.

Now back to the electric field. The electric field, of course, cannot be considered the velocity of the flow of some liquid, but we are entitled to introduce a mathematical concept of the flow, similar to what we described above as the flow of the velocity of the liquid.

Only in the case of an electric field, its flux can be determined by the average normal component of the electric field strength E. In addition, the flux of the electric field can be determined not necessarily through a closed surface, but through any bounded surface of nonzero area S .

Circulation of a vector field

It is well known to everyone that, for greater clarity, fields can be depicted in the form of so-called lines of force, at each point of which the direction of the tangent coincides with the direction of the field strength.

Let's go back to the fluid analogy and imagine the velocity field of the fluid. Let's ask ourselves a question: is the fluid circulating? That is, does it move primarily in the direction of some imaginary closed loop?

For greater clarity, imagine that the liquid in a large container is somehow moving (Fig. A) and we suddenly froze almost all of its volume, but managed to leave the volume unfrozen in the form of a uniformly closed tube in which there is no friction of the liquid on the walls (fig. b).

Outside this tube, the liquid has turned to ice and therefore can no longer move, but inside the tube the liquid is able to continue its movement, provided there is a prevailing momentum that drives it, for example, in a clockwise direction (Fig. . ° C). Then the product of the fluid velocity in the tube and the length of the tube will be called the fluid velocity circulation.

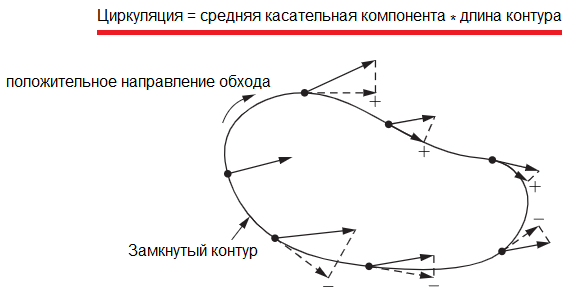
Similarly, we can define a circulation for a vector field, although again the field cannot be said to be the velocity of anything, we can nevertheless define the mathematical characteristic of "circulation" along a contour.

So, the circulation of a vector field along an imaginary closed loop can be defined as the product of the average tangential component of the vector in the direction of the loop's passage — by the length of the loop.