Physical quantities and parameters, scalar and vector quantities, scalar and vector fields

Scalar and vector physical quantities

One of the main goals of physics is to establish the patterns of observed phenomena. For this, when examining different cases, characteristics are introduced that determine the course of physical phenomena, as well as the properties and state of substances and environments. From these characteristics, proper physical quantities and parametric quantities can be distinguished. The latter are defined by so-called parameters or constants.

Actual quantities mean those characteristics of phenomena that determine phenomena and processes and can exist independently of the state of the environment and conditions.

These include, for example, electric charge, field strength, induction, electric current, etc. The environment and the conditions under which the phenomena defined by these quantities occur can change these quantities mainly only quantitatively.

By parameters we mean such characteristics of phenomena that determine the properties of media and substances and influence the relationship between the quantities themselves. They cannot exist independently and are manifested only in their action on the actual size.

Parameters include, for example, electrical and magnetic constants, electrical resistance, coercive force, residual inductance, electrical circuit parameters (resistance, conductance, capacitance, inductance per unit length or volume in a device), etc.

The values ​​of the parameters usually depend on the conditions under which this phenomenon occurs (from temperature, pressure, humidity, etc.), but if these conditions are constant, the parameters keep their values ​​unchanged and are therefore also called constant.

Quantitative (numerical) expressions of quantities or parameters are called their values.

Physical quantities can be defined in two ways: some — only by numerical value, and others — both by numerical value and by direction (position) in space.

The first includes such quantities as mass, temperature, electric current, electric charge, work, etc. These quantities are called scalar (or scalar). A scalar can only be expressed as a single numeric value.

The second quantities, called vector, include length, area, force, velocity, acceleration, etc. of its action in space.

Example (Lorentz force from article Electromagnetic field strength):

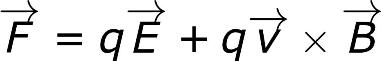
Scalar quantities and absolute values ​​of vector quantities are usually denoted by capital letters of the Latin alphabet, while vector quantities are written with a dash or an arrow above the value symbol.

Scalar and vector fields

Fields, depending on the type of physical phenomenon that characterizes the field, are either scalar or vector.

In mathematical representation, a field is a space, each point of which can be characterized by numerical values.

This concept of a field can also be applied when considering physical phenomena. Then any field can be represented as a space, at each point of which the effect on a certain physical quantity due to the given phenomenon (the source of the field) is established. In this case, the field is given the name of that value.

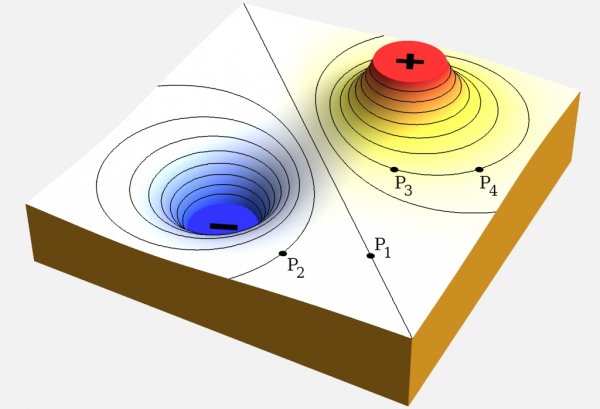
So, a heated body that emits heat is surrounded by a field whose points are characterized by temperature, therefore such a field is called a temperature field. The field surrounding a body charged with electricity, in which a force effect on stationary electric charges is detected, is called an electric field, etc.

Accordingly, the temperature field around the heated body, since temperature can only be represented as a scalar, is a scalar field, and the electric field, characterized by forces acting on charges and having a certain direction in space, is called a vector field.

Examples of scalar and vector fields

A typical example of a scalar field is the temperature field around a heated body. To quantify such a field, at individual points of the picture of this field, you can put numbers equal to the temperature at these points.

However, this way of representing the field is awkward. So they usually do this: they assume that points in space where the temperature is the same belong to the same surface.In this case, such surfaces can be called equal temperatures. The lines obtained from the intersection of such a surface with another surface are called lines of equal temperature or isotherms.

Usually, if such graphs are used, the isotherms are run at equal temperature intervals (for example, every 100 degrees). Then the density of the lines at a given point gives a visual representation of the nature of the field (rate of temperature change).

Example of a scalar field (results of illuminance calculation in the Dialux program):

Examples of a scalar field include the gravitational field (the field of the Earth's gravitational force), as well as the electrostatic field around a body to which an electric charge is given, if each point of these fields is characterized by a scalar quantity called potential.

For the formation of each field you need to spend a certain amount of energy. This energy does not disappear, but accumulates in the field, being distributed throughout its volume. It is potential and can be returned from the field in the form of the work of field forces when masses or charged bodies move in it. Therefore, a field can also be evaluated by a potential characteristic, which determines the field's ability to do work.

Since the energy is usually unevenly distributed in the volume of the field, this characteristic refers to the individual points of the field. The quantity representing the potential characteristic of the field points is called the potential or potential function.

When applied to an electrostatic field, the most common term is "potential", and to a magnetic field, "potential function".Sometimes the latter is also called the energy function.

The potential is distinguished by the following characteristic: its value in the field is continuous, without jumps, it changes from point to point.

The potential of a field point is determined by the amount of work done by the field forces in moving a unit mass or a unit charge from a given point to a point where that field is absent (this characteristic of the field is zero), or that must be expended to action against the field forces to transfer a unit mass or charge to a given point in the field from a point where the action of that field is zero.

Work is scalar, so potential is also scalar.

Fields whose points can be characterized by potential values ​​are called potential fields. Since all potential fields are scalar, the terms «potential» and «scalar» are synonymous.

As in the case of the temperature field discussed above, many points with the same potential can be found in any potential field. The surfaces on which the points of equal potential are located are called equipotential, and their intersection with the plane of the drawing is called equipotential lines or equipotentials.

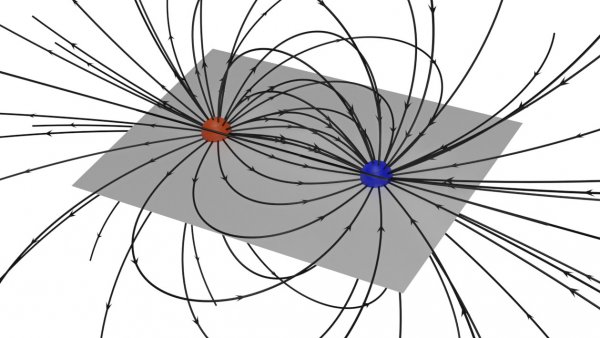
In a vector field, the value characterizing that field at individual points can be represented by a vector whose origin is placed at a given point. To visualize the vector field, one resorts to constructing lines that are drawn so that the tangent at each of its points coincides with the vector characterizing that point.

The field lines, drawn at a certain distance from each other, give an idea of ​​the nature of the field distribution in space (in the region where the lines are thicker, the value of the vector quantity is greater, and where the lines are less frequent, the value is smaller than him).

Eddy and eddy fields

Fields differ not only in the form of the physical quantities that define them, but also in nature, that is, they can be either irrotational, consisting of non-mixing parallel jets (sometimes these fields are called laminar, that is, layered), or vortex (turbulent).

The same rotational field, depending on its characteristic values, can be both scalar-potential and vector-rotational.

The scalar potential will be electrostatic, magnetic and gravitational field if they are determined by the energy distributed in the field. However, the same field (electrostatic, magnetic, gravitational) is vector if it is characterized by forces acting in it.

An eddy-free or potential field always has a scalar potential. An important characteristic of the scalar potential function is its continuity.

An example of a vortex field in the field of electrical phenomena is an electrostatic field. An example of an eddy field is a magnetic field the thickness of a current-carrying wire.

There are so-called mixed vector fields. An example of a mixed field is a magnetic field outside current-carrying conductors (the magnetic field inside these conductors is an eddy field).