Calculation of wire resistance

In practice, it is often necessary to calculate the resistance of different wires. This can be done using formulas or according to the data given in the table. 1.

The influence of the conductor material is taken into account using the resistance indicated by the Greek letter ? and representing wire resistance 1 m length and 1 mm2 cross-sectional area. The lowest resistance? = 0.016 Ohm • mm2 / m silver there is. We give the average value of the specific coNSrotation of some wires:

Silver — 0.016, Lead — 0.21, Copper — 0.017, Nickel — 0.42, Aluminum — 0.026, Manganese — 0.42, Tungsten — 0.055, Constantan — 0.5, Zinc — 0.06, Mercury — 0, 96, Brass — 0.07, Nichrome — 1.05, Steel — 0.1, Fehral -1.2, Phosphor bronze — 0.11, Chromal — 1.45.

With different amounts of impurities and with different ratios of the components that make up rheostat alloys, the resistance can change slightly.

The resistance is calculated by the formula:

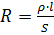
where R is resistance, Ohm; resistance, (Ohm • mm2) / m; l — wire length, m; s — cross-sectional area of ​​the wire, mm2.

If the diameter of the wire d is known, then its cross-sectional area is equal to:

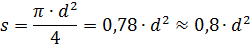
It is best to measure the diameter of the wire using a micrometer, but if it is not there, then you need to tightly wind 10 or 20 turns of wire on a pencil and measure the length of the coil with a ruler. By dividing the length of the coil by the number of turns, we find the diameter of the wire.

To determine the length of wire of a known diameter of a given material required to obtain the desired resistance, use the formula

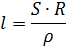
Table 1.

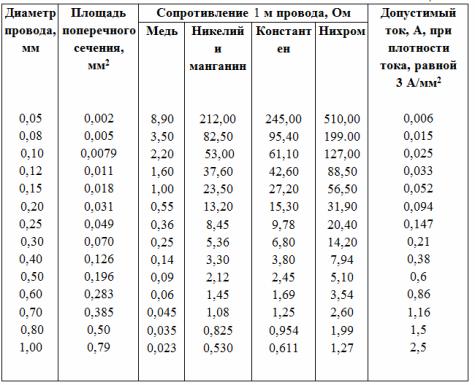
Note. 1. Wire data not listed in the table should be taken as some average values. For example, for a nickel wire with a diameter of 0.18 mm, it can be roughly assumed that the cross-sectional area is 0.025 mm2, the resistance per meter is 18 Ohm, and the permissible current is 0.075 A.

2. For a different value of the current density, the data in the last column should be changed accordingly; for example, at a current density of 6 A / mm2, they should be doubled.

Example 1. Find the resistance of 30 m of copper wire with a diameter of 0.1 mm.

Answer. Determine according to the table. 1 resistance of 1 m of copper wire, it is equal to 2.2 ohms. Therefore, the resistance of 30 m of the wire will be R = 30 • 2.2 = 66 Ohm.

Calculation according to the formulas gives the following results: cross-sectional area of ​​the wire: s = 0.78 • 0.12 = 0.0078 mm2. Since the resistance of copper is 0.017 (Ohm • mm2) / m, we get R = 0.017 • 30 / 0.0078 = 65.50 m.

Example 2.How much 0.5 mm diameter nickel wire is needed to make a rheostat with a resistance of 40 ohms?

Answer. According to the table. 1 we determine the resistance of 1 m of this wire: R = 2.12 Ohm: Therefore, to make a rheostat with a resistance of 40 Ohm, you need a wire whose length is l = 40 / 2.12 = 18.9 m.

Let's do the same calculation using the formulas. We find the cross-sectional area of ​​the wire s = 0.78 • 0.52 = 0.195 mm2. And the length of the wire will be l = 0.195 * 40 / 0.42 = 18.6 m.