Laser — device and principle of operation

Normal behavior of light when passing through a medium

Normally, when light passes through a medium, its intensity decreases. The numerical value of this attenuation can be found from Bouguer's law:

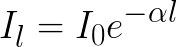
In this equation, in addition to the light intensities I entering and exiting the medium, there is also a factor called the linear light absorption coefficient of the medium. In traditional optics, this coefficient is always positive.

Negative light absorption

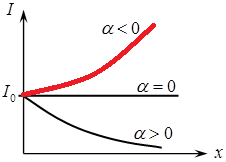
What if for some reason the absorption coefficient is negative? What then? There will be amplification of the light as it passes through the medium; in fact, the medium will show negative absorption.

The conditions for observing such a picture can be created artificially. The theoretical concept regarding the way to the implementation of the proposed phenomenon was formulated in 1939 by the Soviet physicist Valentin Alexandrovich Fabrikant.

In the course of analyzing a hypothetical light-amplifying medium passing through it, Fabrikant proposed the principle of light-amplification. And in 1955the Soviet physicists Nikolai Genadievich Basov and Alexander Mikhailovich Prokhorov applied this Fabrikant idea to the radio frequency region of the electromagnetic spectrum.

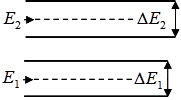
Consider the physical side of the possibility of negative absorption. In an idealized form, the energy levels of atoms can be represented as lines — as if the atoms in each state have only strictly defined energies E1 and E2. This means that when transitioning from state to state, an atom either emits or absorbs exclusively monochromatic light of a precisely defined wavelength.

But reality is far from ideal, and in fact the energy levels of atoms have a certain finite width, that is, they are not lines of exact values. Therefore, during transitions between levels, there will also be a certain range of emitted or absorbed frequencies dv, which depends on the width of the energy levels between which the transition takes place. The values ​​of E1 and E2 can be used to denote only the middle energy levels of the atom.

So, since we have assumed that E1 and E2 are the midpoints of the energy levels, we can consider an atom in these two states. Let E2>E1. An atom can either absorb or emit electromagnetic radiation when it passes between these levels. Suppose that, being in the ground state E1, an atom absorbed external radiation with energy E2-E1 and passed into an excited state E2 (the probability of such a transition is proportional to the Einstein coefficient B12).

Being in an excited state E2, the atom under the action of external radiation with energy E2-E1 emits a quantum with energy E2-E1 and is forced to transition to the ground state with energy E1 (the probability of such a transition is proportional to the Einstein coefficient B21).

If a parallel beam of monochromatic radiation with volume spectral density w (v) passes through a substance whose layer has a unit cross-sectional area and thickness dx, then its intensity will change by the value:

Here n1 is the concentration of atoms in the E1 states, n2 is the concentration of atoms in the E2 states.

Substituting the conditions on the right-hand side of the equation, assuming that B21 = B12, and then substituting the expression for B21, we obtain the equation for the change in light intensity at narrow energy levels:

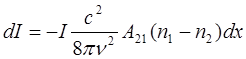
In practice, as mentioned above, the energy levels are not infinitely narrow, so their width must be taken into account. In order not to clutter the article with a description of transformations and a bunch of formulas, we simply note that by entering a frequency range and then integrating over x, we will end up with a formula for finding the real absorption coefficient of an average:

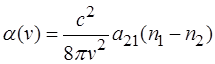
Since it is obvious that under conditions of thermodynamic equilibrium, the concentration n1 of atoms in the lower energy state E1 is always greater than the concentration n2 of atoms in the higher state E2, negative absorption is impossible under normal conditions, it is impossible to amplify light just by going through a real environment without taking any extra measures...

In order for negative absorption to become possible, it is necessary to create conditions when the concentration of atoms in an excited state E2 in the medium will be greater than the concentration of atoms in the ground state E1, that is, it is necessary to organize a reverse distribution of atoms in the medium according to their energy states.

The need for energy pumping of the environment

To organize an inverted population of energy levels (to obtain an active medium) pumping (eg optical or electrical) is used. Optical pumping involves absorption of radiation directed at them by atoms, due to which these atoms go into an excited state.

Electrical pumping in a gas medium involves the excitation of atoms by inelastic collisions with electrons in the gas discharge. According to Fabrikant, some of the low-energy states of atoms must be eliminated by means of molecular impurities.

It is practically impossible to obtain an active medium using optical pumping in a two-level medium, since quantitatively the transitions of atoms per unit time from state E1 to state E2 and vice versa (!) in this case will be equivalent, which means that it is necessary to resort to at least a three-tier system.

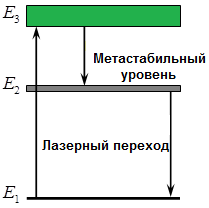
Consider a three-stage pumping system. Let the external radiation with the photon energy E3-E1 act on the medium while the atoms in the medium pass from the state with the energy E1 to the state with the energy E3. From the E3 energy state, spontaneous transitions to the E2 state and to E1 are possible. To obtain an inverted population (when there are more atoms with the E2 level in a given medium), it is necessary to make the E2 level longer-lived than the E3. For this, it is important to comply with the following conditions:

Compliance with these conditions will mean that atoms in the E2 state remain longer, that is, the probability of spontaneous transitions from E3 to E1 and from E3 to E2 exceeds the probability of spontaneous transitions from E2 to E1. Then the E2 level will turn out to be longer lasting, and such a state at the E2 level can be called metastable. Therefore, when light with frequency v = (E3 — E1) / h passes through such an active medium, this light will be amplified. Similarly, a four-level system can be used, then the E3 level will be metastable.

Laser device

Thus, the laser includes three main components: an active medium (in which the population inversion of the energy levels of the atoms is created), a pumping system (a device for obtaining the population inversion) and an optical resonator (which amplifies the radiation many times and forms a directed beam of the output). The active medium can be solid, liquid, gas or plasma.

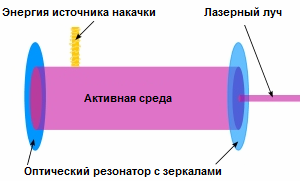
Pumping is done continuously or pulsed. With continuous pumping, the supply of the medium is limited by the overheating of the medium and the consequences of this overheating. In pulsed pumping, the useful energy introduced piecemeal into the medium is obtained more due to the large power of each individual pulse.

Different lasers — different pumping

Solid-state lasers are pumped by irradiating the working medium with powerful gas-discharge flashes, focused sunlight, or another laser. This is always pulsed pumping because the power is so high that the work rod will collapse under continuous action.

Liquid and gas lasers are pumped with an electrical discharge.Chemical lasers assume the occurrence of chemical reactions in their active medium, as a result of which the inverted population of atoms is obtained either from the products of the reaction or from special impurities with an appropriate level structure.

Semiconductor lasers are pumped by forward current through a pn junction or by an electron beam. In addition, there are such pumping methods as photodissociation or gas dynamic method (abrupt cooling of heated gases).

Optical resonator — the heart of the laser

The optical resonator is a system of a pair of mirrors, in the simplest case, two mirrors (concave or parallel) fixed opposite each other, and between them along a common optical axis there is an active medium in the form of a crystal or a cuvette with gas. Photons passing at an angle through the medium leave it at the side, and those moving along the axis, being reflected multiple times, are amplified and exit through a translucent mirror.

This produces laser radiation — a beam of coherent photons — a strictly directed beam. During one passage of light between the mirrors, the magnitude of the gain must exceed a certain threshold — the amount of radiation loss through the second mirror (the better the mirror transmits, the higher this threshold must be).

In order for light amplification to be carried out effectively, it is necessary not only to increase the path of light inside the active medium, but also to ensure that the waves leaving the resonator are in phase with each other, then the interfering waves will give the maximum possible amplitude.

To achieve this goal, it is necessary that each of the waves in the resonator returning to a point on the source mirror and in general, at any point in the active medium, be in phase with the primary wave after an arbitrary number of perfect reflections. This is possible when the optical path traveled by the wave between two returns satisfies the condition:

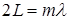
where m is an integer, in this case the phase difference will be a multiple of 2P:

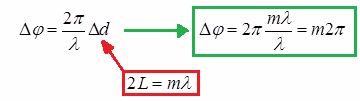
Now, since each of the waves differs in phase from the previous one by 2pi, this means that all the waves leaving the resonator will be in phase with each other, giving maximum amplitude interference. The resonator will have almost monochromatic parallel radiation at the output.

The operation of the mirrors inside the resonator will provide amplification of the modes corresponding to the standing waves inside the resonator; other modes (arising due to the peculiarities of real conditions) will be weakened.

Ruby laser — the first solid state

The first solid-state device was built in 1960 by the American physicist Theodore Maiman. It was a ruby ​​laser (ruby — Al2O3, where some of the lattice sites — within 0.5% — are replaced by triply ionized chromium; the more chromium, the darker the color of the ruby ​​crystal).

The first successful working laser designed by Dr. Ted Mayman in 1960.

A ruby ​​cylinder made of the most homogeneous crystal, with a diameter of 4 to 20 mm and a length of 30 to 200 mm, is placed between two mirrors made in the form of layers of silver applied to the carefully polished ends of this cylinder. A spiral-shaped gas discharge lamp surrounds a cylinder along its entire length and is supplied with high voltage through a capacitor.

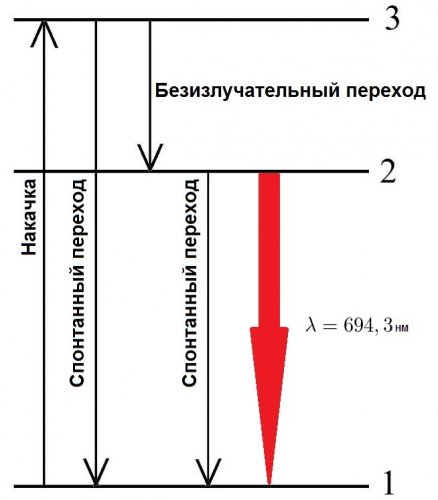
When the lamp is turned on, the ruby ​​is intensely irradiated, while the chromium atoms move from level 1 to level 3 (they are in this excited state for less than 10-7 seconds), this is where the most likely transitions to level 2 are realized — to a metastable level. Excess energy is transferred into the ruby ​​crystal lattice. Spontaneous transitions from level 3 to level 1 are insignificant.

The transition from level 2 to level 1 is forbidden by the selection rules, so the duration of this level is about 10-3 seconds, which is 10,000 times longer than at level 3, as a result, atoms accumulate in ruby with level 2 — this is the reverse population of level 2.

Spontaneously arising during spontaneous transitions, photons can cause forced transitions from level 2 to level 1 and provoke an avalanche of secondary photons, but these spontaneous transitions are random and their photons propagate chaotically, mostly leaving the resonator through its sidewall .

But those of the photons that hit the axis undergo multiple reflections from the mirrors, simultaneously causing the forced emission of secondary photons, which again provoke the stimulated emission, and so on. These photons will move in a direction similar to the primary ones and the flux along the axis of the crystal will increase like an avalanche.

The multiplied flow of photons will exit through the side translucent mirror of the resonator in the form of a strictly directional light beam of colossal intensity. The ruby ​​laser operates at a wavelength of 694.3 nm, while the pulse power can be up to 109 W

Neon laser with helium

The helium-neon (helium / neon = 10/1) laser is one of the most popular gas lasers. The pressure in the gas mixture is about 100 Pa.Neon serves as an active gas, it produces photons with a wavelength of 632.8 nm in continuous mode. The function of helium is to create a reverse population from one of the upper energy levels of neon. The spectrum width of such a laser is about 5 * 10-3 Hz Coherence length 6 * 1011 m, coherence time 2 * 103 ° C.

When a helium-neon laser is pumped, a high-voltage electrical discharge induces the transition of helium atoms to a metastable excited state of the E2 level. These helium atoms collide inelastically with neon atoms in the E1 ground state, transferring their energy. The energy of the E4 level of neon is higher than the E2 level of helium by 0.05 eV. The lack of energy is compensated by the kinetic energy of atomic collisions. As a result, at the E4 level of the neon, an inverted population with respect to the E3 level is obtained.

Types of modern lasers

According to the state of the active medium, lasers are divided into: solid, liquid, gas, semiconductor, and also crystal. According to the pumping method, they can be: optical, chemical, gas discharge. By the nature of the generation, lasers are divided into: continuous and pulsed. These types of lasers emit radiation in the visible range of the electromagnetic spectrum.

Optical lasers appeared later than others. They are capable of generating radiation in the near-infrared range, such radiation (at a wavelength of up to 8 microns) is very suitable for optical communications. Optical lasers contain a fiber in the core of which several ions of suitable rare earth elements have been introduced.

The light guide, as with other types of lasers, is installed between a pair of mirrors.For pumping, laser radiation with the required wavelength is fed into the fiber, so that the ions of the rare earth elements pass into an excited state under its action. Returning to a lower energy state, these ions emit photons with a longer wavelength than that of the initiating laser.

In this way, the fiber acts as a source of laser light. Its frequency depends on the type of rare earth elements added. The fiber itself is made of heavy metal fluoride, which results in the efficient generation of laser radiation at the frequency of the infrared range.

X-ray lasers occupy the opposite side of the spectrum — between ultraviolet and gamma — these are orders of magnitudes with wavelengths from 10-7 to 10-12 m. Lasers of this type have the highest pulse brightness of all types of lasers.

The first X-ray laser was built in 1985 in the USA, at the Livermore Laboratory. Lawrence. The laser generated on selenium ions, the wavelength range is from 18.2 to 26.3 nm, and the highest brightness falls on the wavelength line of 20.63 nm. Today, laser radiation with a wavelength of 4.6 nm has been achieved with aluminum ions.

The X-ray laser is generated by pulses with a duration of 100 ps to 10 ns, which depends on the lifetime of the plasma formation.

The fact is that the active medium of an X-ray laser is a highly ionized plasma, which is obtained, for example, when a thin film of yttrium and selenium is irradiated with a high-power laser in the visible or infrared spectrum.

The energy of the X-ray laser in a pulse reaches 10 mJ, while the angular divergence in the beam is approximately 10 milliradians. The ratio of pump power to direct radiation is about 0.00001.