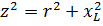Impedance of AC circuits

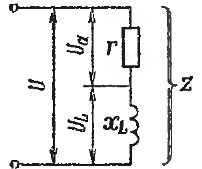
When devices with active and inductive resistance are connected in series (Fig. 1), the total resistance of the circuit cannot be found by arithmetic summation. If we denote the impedance by z, then the formula is used to determine it:

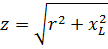
As you can see, impedance is the geometric sum of active and reactive resistance. So for example, if r = 30 Ohm and XL = 40 Ohm, then

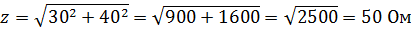
i.e. z turned out to be less than r + XL = 30 + 40 = 70 ohms.

To simplify the calculations, it is useful to know that if one of the resistances (r or xL) exceeds the other by a factor of 10 or more, then you can ignore the lower resistance and assume that z is equal to the higher resistance. The error is very small.

For example, if r = 1 Ohm and xL = 10 Ohm, then

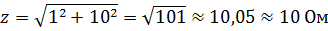
An error of only 0.5% is perfectly acceptable, since the resistances r and x themselves are known with less accuracy.

So if

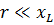
Che

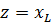
what if

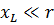
Che

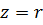
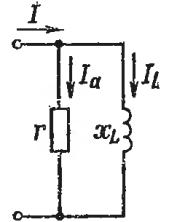
When connecting branches with active and reactive resistance in parallel (Fig. 2), it is more convenient to calculate the impedance using active conductivity

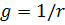
and reactive conductance

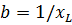
The total conductance of the circuit y is equal to the geometric sum of the active and reactive conductances:

And the total resistance of the circuit is the reciprocal of y,

If we express the conductivity in terms of resistances, then it is easy to obtain the following formula:

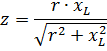
This formula resembles the well-known formula

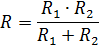
but only the denominator contains not the arithmetic but the geometric sum of the branch resistances.

An example. Find the total resistance if devices with r = 30 He and xL = 40 Ohm are connected in parallel.

Answer.

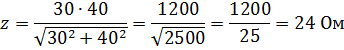
When calculating z for a parallel connection, for simplicity, a large resistance can be neglected if it exceeds the smallest by a factor of 10 or more. The error will not exceed 0.5%

Rice. 1. Series connection of sections of circuits with active and inductive resistance

Rice. 2. Parallel connection of sections of a circuit with active and inductive resistance

Therefore, if

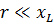
Che

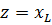
what if

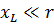
Che

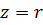
The principle of geometric addition is used for alternating current circuits and in cases where it is necessary to add active and reactive voltages or currents. For a series circuit according to fig. 1 the voltages are added:

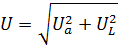
When connected in parallel (Fig. 2), the currents are added:

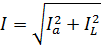
If devices that have only one active resistance or only one inductive resistance are connected in series or parallel, then the addition of resistances or conductances and the corresponding voltages or currents, as well as active or reactive power, is done arithmetically.

For any AC circuit, Ohm's law can be written in the following form:

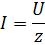
where z is the impedance calculated for each link as shown above.

The power factor cosφ for each circuit is equal to the ratio of the active power P to the total S. In a series connection, this ratio can be replaced by the ratio of voltages or resistances:

With a parallel connection we get:

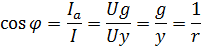
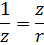
The derivation of the basic formulas for designing a series AC circuit with active and inductive resistance can be done as follows.

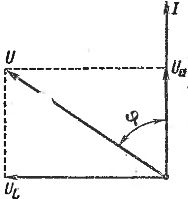
The easiest way to build a vector diagram for a series circuit (Fig. 3).

Rice. 3. Vector diagram for a series circuit with active and inductive resistance

This diagram shows the current vector I, the voltage vector UA in the active section coincident in direction with the vector I, and the voltage vector UL at the inductive resistance. This voltage is 90° ahead of the current (recall that the vectors must be considered rotating counterclockwise). The total stress U is the total vector, i.e. the diagonal of a rectangle with sides UA and UL. In other words, U is the hypotenuse and UA and UL are the legs of a right triangle. It follows that

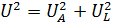
This means that the voltages in the active and reactive sections add up geometrically.

Dividing both sides of the equality by I2, we find the formula for the resistances:

or