AC mathematical expression
Alternating current can be expressed mathematically using the equation:
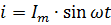
where ω is the angular frequency equal to
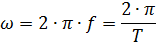
Using this equation, you can find the instantaneous value of the alternating current at any time t. The value ωt below the sinusoidal sign defines these instantaneous current values and is the phase angle (or phase). It is expressed in radians or degrees.
For an alternating sinusoidal voltage or for an EMF, you can write the same equations:
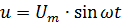
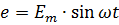
In all the above equations, instead of sine, you can put the cosine. Then the initial moment (at t = 0) will correspond to the amplitude phase, not zero.
We will use the alternating current equation to determine the power of this current and prove the relationship between amplitude and average values.
The instantaneous power of alternating current, i.e. its power at any time is equal to
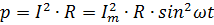
According to the formula
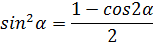
we present the expression for the degree in the following form:
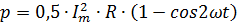
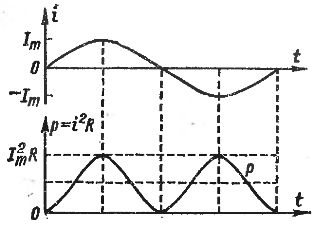
The resulting formula shows that the power oscillates at twice the frequency. This is not difficult to understand.After all, the power at a constant resistance R is determined only by the magnitude of the current i and does not depend on the direction of the current. The resistance is heated in each direction of the current. The power formula reflects this by the fact that i2 is always positive, regardless of the sign of the current. Therefore, in one period the power twice becomes equal to zero (when i = 0) and twice reaches its maximum value (when i = Im and i = — Im), that is, it changes with twice the frequency compared to the frequency from the current itself.
Let us now find the average value (ie the arithmetic mean) of the AC power over one period. Mean cos ωt in one period (or for an integer number of periods) is equal to zero, since the cosine takes a number of positive values in one half-period and exactly the same negative values in the other half-period. It is clear that the arithmetic mean of all these values is zero, and the expression Im2R / 2 is a constant value. It also represents the average AC power over one half-cycle or an integer number of half-cycles.
If we imagine that Im2 / 2 is the square of the average value of the alternating current I, that is, write I2 = I am2/ 2, then we get from here:
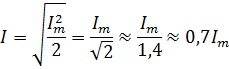
The above relationships can be illustrated. In fig. 1 graphs given alternating current i and its instantaneous power p.
Rice. 1. Change in instantaneous AC power over one period
The power plots show that p indeed oscillates with double frequency from 0 to Im2R, and the average power value marked by the bold dashed line is Im2R / 2