What is magnetomotive force, Hopkinson's law

In the second half of the 19th century, the English physicist John Hopkinson and his brother Edward Hopkinson, developing the general theory of magnetic circuits, derived a mathematical formula called "Hopkinson's formula" or Hopkinson's law, which is an analogue of Ohm's law (used to calculate of electrical circuits).

So, if Ohm's classical law mathematically describes the relationship between current and electromotive force (EMF), Hopkinson's law similarly expresses the relationship between magnetic flux and the so-called magnetomotive force (MDF).

As a result, it turned out that magnetomotive force is a physical quantity that characterizes the ability of electric currents to create magnetic fluxes. And Hopkinson's law in this regard can be successfully used in the calculations of magnetic circuits, since the MDF in magnetic circuits is analogous to the EMF in electric circuits. The date of discovery of Hopkinson's law is considered to be 1886.

The magnitude of the magnetomotive force (MDF) is initially measured in amperes or, if we are talking about a coil with a current or an electromagnet, then for the convenience of calculations use its expression in ampere-turns:

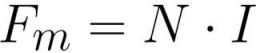
where: Fm is the magnetomotive force in the coil [ampere * turn], N is the number of turns in the coil [turn], I is the amount of current in each of the turns of the coil [ampere].

If you enter the magnetic flux value here, then Hopkinson's law for the magnetic circuit will take the form:

where: Fm is the magnetomotive force in the coil [ampere * turn], F is the magnetic flux [weber] or [henry * ampere], Rm is the magnetic resistance of the magnetic flux conductor [ampere * turn / weber] or [ turn / henry] .

The textual formulation of Hopkinson's law was originally as follows: "in an unbranched magnetic circuit, the magnetic flux is directly proportional to the magnetomotive force and inversely proportional to the total magnetic resistance." That is, this law determines the relationship between magnetomotive force, reluctance and magnetic flux in the circuit:

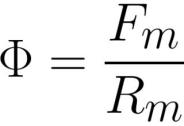
here: F is the magnetic flux [weber] or [henry * ampere], Fm is the magnetomotive force in the coil [ampere * revolution], Rm is the magnetic resistance of the magnetic flux conductor [ampere * revolution / weber] or [ turn / henry] .

Here it is important to note that in fact the magnetomotive force (MDF) has a fundamental difference from the electromotive force (EMF), which consists in the fact that no particles move directly in the magnetic flux, while the current arising under the action of the EMF takes the movement of charged particles, for example electrons in metal wires. However, the idea of ​​MDS helps solve the problems of calculating magnetic circuits.

Consider, for example, an unbranched magnetic circuit that includes a yoke of cross-sectional area S, the same throughout its length, and the material of the yoke has a magnetic permeability mu.

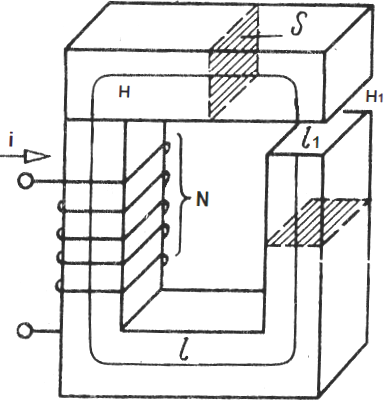
Gap in yoke - different material, magnetic permeability which mu1. The coil placed on the yoke contains N turns, a current i flows through each of the turns of the coil. We apply the magnetic field circulation theorem to the centerline of the yoke:

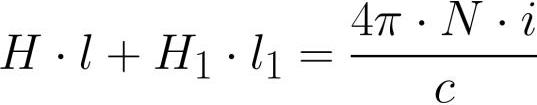
where: H is the magnetic field strength inside the yoke, H1 is the magnetic field strength inside the gap, l is the centerline length of the yoke induction (without the gap), l1 is the length of the gap.

Since the magnetic flux inside the yoke and inside the gap has the same value (due to the continuity of the magnetic induction lines), after writing Ф = BS and В = mu * H, we will write down the magnetic field strength in more detail, and after substitute this into the above formula:

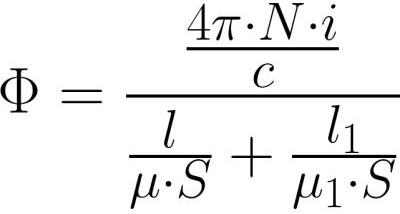
It is easy to see that, like the EMF in Ohm's law for electrical circuits, the MDS

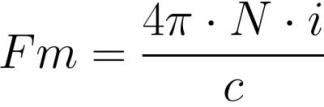
here plays the role of electromotive force and magnetic resistance

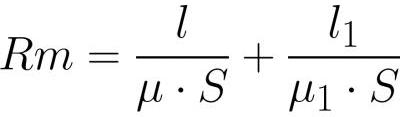
the role of resistance (by analogy with classical Ohm's law).