Theory of automata, finite automata
The structure, design, principle of operation of various machines are largely determined by its functional purpose. Distinguish between technological, transport, computing, military and other machines. Entire automatic complexes designed to perform complex technological processes are widely introduced in various industries. Automata are designed and built that perform various logical functions (logical machines).
Theory of automata — cybernetics section, which arose under the influence of the requirements of the technology of digital computers and control machines. Discrete automata studied in automata theory are abstract models of real systems (both technical and biological) that process discrete (digital) information at discrete time steps.
Automata theory is based on precise mathematical concepts that formalize intuitive ideas about the functioning (behavior) of the automaton and about its structure (internal structure).
In this case, information transformation is always understood as an operation that transforms input sequences composed of letters from the input alphabet into output sequences composed of letters from the output alphabet.
The apparatus of mathematical logic, algebra, probability theory, combinatorics and graph theory is widely used.
The problem with the theory of automata in some of its parts (structural theory of automata) grew from the theory of relay-contact circuits, which began to take shape in the late 1930s. inclusive methods of logical algebra.

In the structural theory of automata, different types of schemes are studied, designed to describe how a complex automaton is created from simpler components (elements) properly connected in a system.
Another direction, called the abstract theory of automata, studies the behavior of automata (that is, the nature of the transformation of information carried out by them), while abstracting from the specifics of their internal structure, and arose in the 1950s.
Within the framework of the abstract theory of automata, the content of the concepts "automaton" and "machine" is essentially exhausted by the standard description of the transformation of information that is carried out by an automaton. Such a transformation can be deterministic, but it can also be probabilistic in nature.
The most studied are deterministic machines (automata), which include finite automata — the main object of study in the theory of automata.
A finite state machine is characterized by a limited amount of memory (the number of internal states) and is defined using a transition function.With some reasonable idealization, all modern mathematical machines and even the brain, from the point of view of their functioning, can be regarded as finite automata.
The terms "sequential machine", "Milly automaton", "Moore automaton" are used in the literature (and not uniformly by all authors) as synonyms of the term "finite automaton" or to emphasize certain features in the transition functions of a finite automaton.
Automata with unlimited memory is a Turing machine capable of performing (potentially) any efficient information transformation. The concept of "Turing machine" arose earlier than the concept of "finite state machine" and is mainly studied in the theory of algorithms.
Abstract automata theory is closely related to well-known algebraic theories, for example semigroup theory. From an applied point of view, the results characterizing the transformation of information in an automaton in terms of memory size are of interest.
This is the case, for example, in problems with experiments on automata (works by E.F. Moore, etc.), where one or another information about the transition functions of the automaton or about the capacity of its memory is obtained from the results of the experiments.
Another task is to calculate the periods of the output sequences, based on the available information about the memory size of the automaton and the periods of the input sequences.
Of great importance is the development of methods for minimizing the memory of finite state machines and studying their behavior in random environments.
In abstract automata theory, the synthesis problem is the following.In terms of some clearly formalized language, the conditions are written for the behavior of the designed automaton (for the event represented in the automaton). In this case, it is necessary to develop methods that according to each written condition:
1) find out whether there exists such a state machine that the information transformed by it meets this condition;
2) if yes, then the transition functions of such a finite state machine are constructed or its memory size is estimated.
The solution of the synthesis task in such a formulation presupposes the preliminary creation of a convenient language for recording the operating conditions of an automaton with convenient algorithms for the transition from recording to transitive functions.
In the structural theory of automata, the synthesis problem consists in constructing a chain of elements of a given type that realizes a finite automaton given by its transition functions. In this case, they usually state some optimality criterion (for example, the minimum number of elements) and seek to obtain an optimal scheme.
As it turned out later, this means that some of the methods and concepts developed earlier in relation to relay-contact circuits are applicable to circuits of another type.
In connection with the development of electronic technologies, the most widespread are the schemes of functional elements (logical networks). A special case of logic networks are abstract neural networks, whose elements are called neurons.
Many methods of synthesis have been developed, depending on the type of circuits and the transformation of information for which they are intended (Synthesis of relay devices).
Look -Minimization of combinational circuits, Carnot maps, circuit synthesis
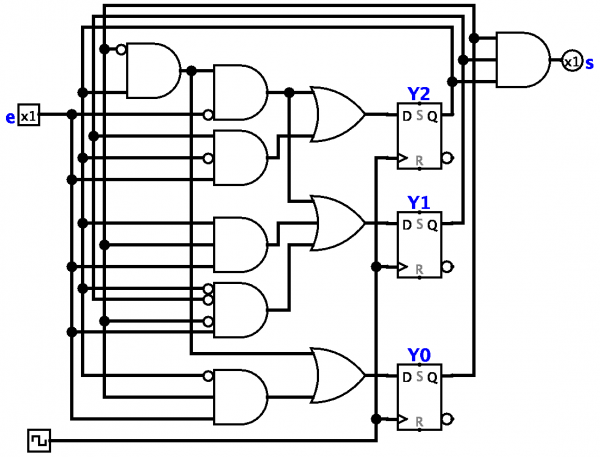
Finite state machine — a mathematical model of a control system with a fixed (incapable of increasing during operation) memory size.
The concept of a finite state machine is a mathematical abstraction that characterizes the general characteristics of a set of control systems (for example, a multi-loop relay device). All such systems have common features that are natural to accept as the definition of a finite automaton.
Every completed automaton has an entrance exposed to external influences and internal elements. For both input and internal elements, there is a fixed number of discrete states that they can take.
The change in the states of the input and internal elements occurs at discrete moments in time, the intervals between which are called ticks. The internal state (the state of the internals) at the end of the tape is determined entirely by the internal state and the state of the input at the beginning of the tape.
All other definitions of a finite automaton can be reduced to this characteristic, in particular definitions that assume that a finite automaton has an output that depends on the internal state of the automaton at a given time.
In terms of such a characteristic, the nature of its inputs and internal states is irrelevant to the description of a complete automaton. Instead of inputs and states, you can just look at their numbers in a random numbering.
The state machine will be set if the dependence of its internal state number on the previous internal state number and the previous input state number is specified. Such a task can be in the form of a final table.
Another common way to define a complete automaton is the construction of the so-called transition diagrams. Input states are often called simply inputs, and internal states are simply states.
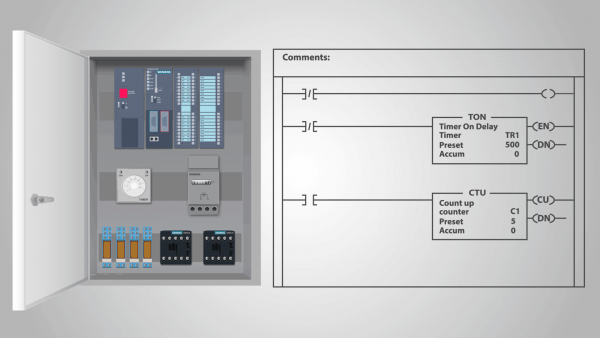
A finite state machine can be a model of both technical devices and some biological systems. Automata of the first type are, for example, relay devices and various electronic computers, incl. programmable logic controllers.
In the case of a relay device, the role of input states is played by combinations of states of the sensitive elements of the relay device (each combination of such states is a «complex state», characterized by an indication of all the sensitive elements of these discrete states that they have in a given moment). Similarly, combinations of states of intermediate elements of a relay device act as internal states.
A programmable logic controller (PLC) is an example of a relay action device that can be called a stand-alone state machine.
In fact, once the program has been entered into the PLC and the controller has begun to calculate, it is not exposed to external influences and each subsequent state is completely determined by its previous state. We can assume that the input has the same state in every clock cycle.
Conversely, any finite state machine that has the only possible input state is naturally called autonomous, since in this case the external environment carries no information that controls its behavior.
See also:
The use of microprocessor systems in electrical engineering on the example of the use of PLC