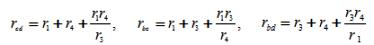Calculation of direct current circuits
Calculation of simple DC circuits

Equivalent transformations in an electric circuit mean replacing some elements with others in such a way that the electromagnetic processes in it do not change and the circuit is simplified. One of the types of such transformations is the replacement of several consumers connected in series or in parallel with one equivalent.
Several consumers connected in series can be replaced by one and its equivalent resistance is equal to the sum of the resistances of the consumers, included in a series… For n users you can write:
rе = r1 + r2 + … + rn,
where r1, r2, …, rn are the resistances of each of the n consumers.
When n consumers are connected in parallel, the equivalent conductivity ge is equal to the sum of the conductivities of individual elements connected in parallel:
ge = g1 + g2 + … + gn.
Given that conductance is the reciprocal of resistance, the equivalent resistance can be determined by the expression:
1 / rе = 1 / r1 + 1 / r2 + … + 1 / rn,
where r1, r2, …, rn are the resistances of each of the n consumers connected in parallel.
In the particular case where two consumers r1 and r2 are connected in parallel, the equivalent resistance of the circuit is:
rе = (r1 x r2) / (r1 + r2)
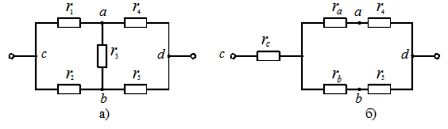
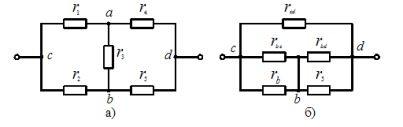
Transformations in complex circuits where there is no apparent form serial and parallel connection elements (Figure 1), begin by replacing the elements included in the original delta circuit with equivalent star-connected elements.
Figure 1. Transformation of circuit elements: a — connected by a triangle, b — in an equivalent star
In Figure 1, a triangle of elements is formed by users r1, r2, r3. In Figure 1b, this triangle is replaced by equivalent star-connected elements ra, rb, rc. To prevent potentials from changing at points a, b of the circuit, the resistances of equivalent users are determined by the expressions:
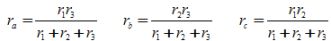
Simplification of the original circuit can also be done by replacing the star-connected elements with a circuit in which users connected by a triangle.
In the scheme shown in figure 2, a, it is possible to separate a star formed by consumers r1, r3, r4. These elements are included between points c, b, d. In Figure 2b, between these points there are equivalent consumers rbc, rcd, rbd connected by a triangle. The resistances of equivalent consumers are determined by the expressions:
Figure 2.Transformation of the circuit elements: a — star-connected, b — in an equivalent triangle
Further simplification of the schemes shown in Figures 1, b and 2, b can be done by replacing sections with serial and parallel connection of elements from their equivalent consumers.
In the practical implementation of the method of calculating a simple circuit using transformations, sections with parallel and series connection of consumers are identified in the circuit, and then the equivalent resistances of these sections are calculated.
If there are no such sections explicitly in the original circuit, then, applying the above-described transitions from triangle of elements to star or from star to triangle, they are manifested.
These operations simplify the circuit. By applying them several times, they arrive at a form with one source and one equivalent consumer of energy. Also, application Ohm's and Kirchhoff's laws, calculation of currents and voltages in circuit sections.
Calculation of complex DC circuits
During the calculation of a complex circuit, it is necessary to determine some electrical parameters (mainly currents and voltages on the elements) based on the initial values specified in the problem statement. In practice, several methods are used to calculate such schemes.
To determine the branch currents, you can use: a method based on direct application Kirchhoff's laws, current cycle method, method of nodal stresses.
To check the correctness of the calculation of the currents, it is necessary to do capacity balance… From law of conservation of energy it follows that the algebraic sum of the powers of all power supplies in the circuit is equal to the arithmetic sum of the powers of all consumers.
The power of a power source is equal to the product of its emf by the amount of current flowing through that source. If the direction of the emf and the current in the source coincide, then the power is positive. Otherwise, it is negative.
The power of the consumer is always positive and is equal to the product of the square of the current in the consumer by the value of its resistance.
Mathematically, the power balance can be written as follows:

where n is the number of power supplies in the circuit; m is the number of users.
If the power balance is maintained, the current calculation is correct.
In the process of drawing up the power balance, you can find out in what mode the power supply is working. If its power is positive, then it supplies power to an external circuit (such as a battery in discharge mode). At a negative value of the power of the source, the latter consumes energy from the circuit (the battery in charging mode).