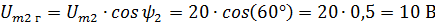A symbolic method for calculating AC circuits

A symbolic method of operations with vector quantities is based on a very simple idea: each vector is decomposed into two components: one horizontal, passing along the abscissa, and the second, vertical, passing along the ordinate. In this case, all the horizontal components follow a straight line and can be added by simple algebraic addition, and the vertical components are added in the same way.

This approach generally results in two resultant components, a horizontal and a vertical, which are always adjacent to each other at the same 90° angle.

These components can be used to find the result, that is, for geometric addition. The right-angled components represent the legs of a right triangle, and their geometric sum represents the hypotenuse.

You can also say that the geometric sum is numerically equal to the diagonal of a parallelogram built on the components as well as on its sides... If the horizontal component is denoted by AG and the vertical component by AB, then the geometric sum (1)

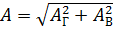
Finding the geometric sum of right triangles is much easier than oblique triangles. It is easy to see that (2)

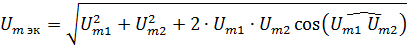
becomes (1) if the angle between the components is 90 °. Since cos 90 = 0, the last term in the radical expression (2) disappears, as a result of which the expression is greatly simplified. Note that one of three words must be added before the word "sum": "arithmetic", "algebraic", "geometric".

Fig. 1.

The word "amount" without specifying which leads to uncertainty and in some cases to gross errors.

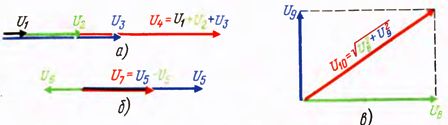
Recall that the resulting vector is equal to the arithmetic sum of the vectors in the case when all the vectors go along a straight line (or parallel to each other) in the same direction. In addition, all vectors have a plus sign (Fig. 1, a).

If the vectors go along a straight line but point in opposite directions, then their result is equal to the algebraic sum of vectors, in which case some terms have a plus sign and others have a minus sign.

For example, in the diagram of fig. 1, b U6 = U4 — U5. We can also say that the arithmetic sum is used in cases where the angle between the vectors is zero, algebraic when the angles are 0 and 180 °. In all other cases, the addition is carried out vectorially, that is, the geometric sum is determined (Fig. 1, c).

Example... Determine the parameters of the equivalent sine wave for the circuit Fig. 2, but symbolic.

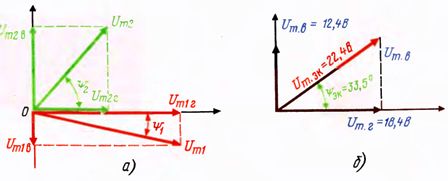
Answer. Let's draw vectors Um1 Um2 and decompose them into components. It can be seen from the drawing that each horizontal component is the vector value multiplied by the cosine of the phase angle, and the vertical is the vector value multiplied by the sine of the phase angle. Then

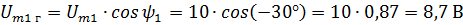
Fig. 2.

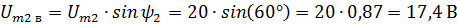
Obviously, the total horizontal and vertical components are equal to the algebraic sums of the corresponding components. Then

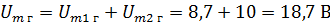
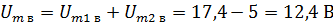
The resulting components are shown in Fig. 2, b. Determine the value of Um for this, calculate the geometric sum of the two components:

Determine the equivalent phase angle ψeq. Fig. 2, b, it can be seen that the ratio of the vertical to the horizontal component is the tangent of the equivalent phase angle.

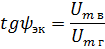
where

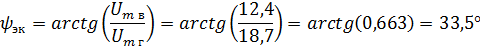
The sinusoid thus obtained has an amplitude of 22.4 V, an initial phase of 33.5 ° with the same period as the components. Note that only sine waves of the same frequency can be added, because when adding sine curves of different frequencies the resulting curve ceases to be sine and all concepts applicable only to harmonic signals become invalid in this case.

Let us retrace once more the entire chain of transformations that must be made with the mathematical descriptions of the harmonic waveforms when performing various calculations.

First, the temporal functions are replaced by vector images, then each vector is decomposed into two mutually perpendicular components, then the horizontal and vertical components are calculated separately, and finally the values ​​of the resulting vector and its initial phase are determined.

This method of calculation eliminates the need to graphically add (and in some cases perform more complex operations, for example, multiply, divide, extract roots, etc.) sinusoidal curves and resort to calculations using the formulas of oblique triangles.

However, it is rather cumbersome to calculate the horizontal and vertical components of the operation separately.In such calculations, it is very convenient to have such a mathematical apparatus with which you can calculate both components at once.

Already at the end of the last century, a method was developed that allows simultaneous calculations of numbers plotted on mutually perpendicular axes. The numbers on the horizontal axis were called real, and the numbers on the vertical axis were called imaginary. When calculating these numbers, a factor of ± 1 is added to the real numbers, and ± j to the imaginary numbers (read "xi"). Numbers consisting of real and imaginary parts are called complex, and the method of calculations performed with their help is symbolic.

Let us explain the term «symbolic». The functions to be computed (harmonics in this case) are originals, and those expressions that replace the originals are images or symbols.

When using the symbolic method, all calculations are performed not on the originals themselves, but on their symbols (images), which in our case represent the corresponding complex numbers, since it is much easier to perform operations on images than on the originals themselves.

After all image operations are completed, the original corresponding to the resulting image is recorded on the resulting image. Most of the calculations in electrical circuits are done using the symbolic method.