Calculation of the shunt for the ammeter

Concepts and formulas

A shunt is a resistance that is connected across the ammeter terminals (in parallel with the instrument's internal resistance) to increase the measurement range. The measured current I is divided between measuring shunt (rsh, Ish) and ammeter (ra, Ia) inversely proportional to their resistances.

Shunt resistance rsh = ra x Ia / (I-Ia).

To increase the measurement range by n times, the shunt should have a resistance rsh = (n-1) / ra

Examples of

1. The electromagnetic ammeter has internal resistance ra = 10 Ohm, and the measurement range is up to 1 A. Calculate the shunt resistance rsh so that the ammeter can measure current up to 20 A (Fig. 1).

Rice. 1.

The measured current of 20 A will split into a current Ia = 1 A that will flow through the ammeter and a current Ish that will flow through the shunt:

I = Ia + Ish.

Therefore, the current flowing through the shunt, Ish = I-Ia = 20-1 = 19 A.

The measured current I = 20 A must be divided in the ratio Ia: Ish = 1: 19.

It follows that the branch resistances must be inversely proportional to the currents: Ia: Ish = 1 / ra: 1 / rsh;

Ia: Ish = rsh: ra;

1: 19 = rw: 10.

Shunt resistance rsh = 10/19 = 0.526 Ohm.

The shunt resistance must be 19 times less than the ammeter resistance ra so that the current Ish passes through it, which is 19 times greater than the current Ia = 1 A that passes through the ammeter.

2. The magnetoelectric milliammeter has a non-shunt measuring range of 10 mA and an internal resistance of 100 Ohm. What resistance should the shunt have if the device is to measure current up to 1 A (Fig. 2)?

Rice. 2.

At full deflection of the needle, the current Ia = 0.01 A will pass through the coil of the milliammeter and through the shunt Ish:

I = Ia + Ish,

whence Ish = I-Ia = 1-0.99 A = 990 mA.

The current 1 A will be divided in inverse proportion to the resistances: Ia: Ish = rsh: ra.

From this ratio we find the shunt resistance:

10: 990 = rsh: 100; rsh = (10×100) / 990 = 1000/990 = 1.010 Ohms.

At full deflection of the arrow, current Ia = 0.01 A will pass through the device, current Ish = 0.99 A through the shunt and current I = 1 A.

When measuring the current I = 0.5 A, the current Ish = 0.492 A will pass through the shunt and the current Ia = 0.05 A will pass through the ammeter. The arrow deviates to half scale.

For any current from 0 to 1 A (with the selected shunt), the currents in the branches are divided in the ratio ra: rsh, i.e. 100: 1.01.

3. The ammeter (Fig. 3) has an internal resistance rа = 9.9 Ohm, and the resistance of its shunt is 0.1 Ohm. What is the ratio of the measured current of 300 A in the device and the shunt?

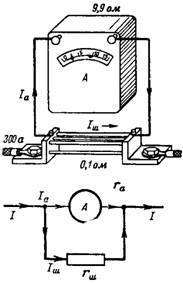
Rice. 3.

We will solve the problem using Kirchhoff's first law: I = Ia + Ish.

Also, Ia: Ish = rsh: ra.

From here

300 = Ia + Ish;

Ia: Ish = 0.1: 9.9.

From the second equation we obtain the current Ia and substitute it in the first equation:

Ia = 1 / 99xIsh;

300 = 1 / 99xIsh + Ish;

Ishx (1 + 1/99) = 300;

Ishx100 / 99 = 300;

Ish = 300 / 100×99 = 297 A.

The current in the device Ia = I-Ish = 300-297 = 3 A.

From the total measured current, current Ia = 3 A will pass through the ammeter, and Ish = 297 A through the shunt.

Ammeter shunt

4. An ammeter whose internal resistance is 1.98 Ohm gives a full deflection of the arrow at a current of 2 A. It is necessary to measure the current up to 200 A. What resistance should a shunt connected in parallel to the terminals of the device have?

In this task, the measurement range is increased by a factor of 100: n = 200/2 = 100.

The required resistance of the shunt rsh = rа / (n-1).

In our case, the shunt resistance will be: rsh = 1.98 / (100-1) = 1.98 / 99 = 0.02 Ohm.