Dielectric strength of the insulation. Calculation examples

With a gradual increase in the voltage U between conductors separated by a dielectric (insulation), for example, capacitor plates or conducting cable wires, the intensity (strength) of the electric field in the dielectric increases. The strength of the electric field in the dielectric also increases as the distance between the wires decreases.

At a certain field strength, a breakdown occurs in the dielectric, a spark or arc is formed and an electric current appears in the circuit. The strength of the electric field at which the breakdown of the insulation occurs is called the electrical strength Epr of the insulation.

Dielectric strength is defined as voltage per mm of insulation thickness and is measured in V/mm (kV/mm) or kV/cm. For example, the dielectric strength of air between smooth plates is 32 kV / cm.

The strength of the electric field in a dielectric for the case when the conductors are in the form of plates or strips separated by an equal gap (for example, in a paper capacitor) is calculated by the formula

E = U / d,

where U is the voltage between the wires, V (kV); d — thickness of the dielectric layer, mm (cm).

Examples of

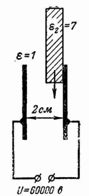
1. What is the electric field strength in the 3 cm thick air gap between the plates if the voltage between them is U = 100 kV (Fig. 1)?

Rice. 1.

The electric field strength is: E = U / d = 100000/3 = 33333 V / cm.

Such a voltage exceeds the dielectric strength of air (32 kV / cm) and there is a risk of destruction.

The risk of DC damage can be prevented by increasing the gap to, for example, 5 cm, or by using other, stronger insulation instead of air, such as electrical cardboard (Fig. 2).

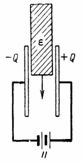
Rice. 2.

Electrical cardboard has a dielectric constant of ε = 2 and a dielectric strength of 80,000 V/cm. In our case, the electric field strength in the insulation is 33333 V. Air cannot withstand this force, while the electrical cardboard in this case has a reserve of dielectric strength of 80,000/33333 = 2.4, since the dielectric strength of the electrical box is 80,000/32,000 = 2.5 times that of air.

2. What is the electric field strength in the dielectric of a capacitor 3 mm thick if the capacitor is connected to a voltage U = 6 kV?

E = U / d = 6000 / 0.3 = 20000 V / cm.

3. A dielectric with a thickness of 2 mm breaks down at a voltage of 30 kV. What was its electrical strength?

E = U / d = 30,000 / 0.2 = 150,000 V / cm = 150 kV / cm. Glass has such an electrical strength.

4. The space between the plates of the capacitor is filled with layers of electrical cardboard and a layer of mica of the same thickness (Fig. 3). The voltage between the plates of the capacitor is U = 10000 V. The electrical cardboard has a dielectric constant ε1 = 2 and mica ε2 = 8.How will the voltage U be distributed between the layers of insulation and what intensity will the electric field have in the individual layers?

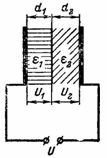
Rice. 3.

The voltages U1 and U2 across dielectric layers of the same thickness will not be equal. The capacitor voltage will be divided into voltages U1 and U2, which will be inversely proportional to the dielectric constants:

U1 / U2 = ε2 / ε1 = 8/2 = 4/1 = 4;

U1 = 4 ∙ U2.

Since U = U1 + U2, we have two equations with two unknowns.

Substitute the first equation into the second: U = 4 ∙ U2 + U2 = 5 ∙ U2.

Therefore, 10000 V = 5 ∙ U2; U2 = 2000 V; U1 = 4, U2 = 8000V.

Although the dielectric layers are the same thickness, they are not equally charged. A dielectric with a higher dielectric constant is less loaded (U2 = 2000 V) and vice versa (U1 = 8000 V).

The electric field strength E in the dielectric layers is equal to:

E1 = U1 / d1 = 8000 / 0.2 = 40,000 V / cm;

E2 = U2 / d2 = 2000 / 0.2 = 10000 V / cm.

The difference in the dielectric constant leads to an increase in the electric field strength. If the entire gap were filled with only one dielectric, for example, mica or electrical cardboard, the electric field strength would be smaller, since it would be distributed fairly evenly in the gap:

E = U / d = (U1 + U2) / (d1 + d2) = 10000 / 0.4 = 25000 V / cm.

It is therefore necessary to avoid the use of complex insulation with very different dielectric constants. For the same reason, the risk of failure increases when air bubbles form in the insulation.

5. Determine the strength of the electric field in the capacitor dielectric from the previous example if the thickness of the dielectric layers is not the same.The electrical board has a thickness d1 = 0.2 mm and mica d2 = 3.8 mm (Fig. 4).

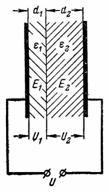
Rice. 4.

The electric field strength will be distributed inversely proportional to the dielectric constants:

E1 / E2 = ε2 / ε1 = 8/2 = 4.

Since E1 = U1 / d1 = U1 / 0.2 and E2 = U2 / d2 = U2 / 3.8, then E1 / E2 = (U1 / 0.2) / (U2 / 3.8) = (U1 ∙ 3.8) / (0.2 ∙ U2) = 19 ∙ U1 / U2.

Therefore E1 / E2 = 4 = 19 ∙ U1 / U2, or U1 / U2 = 4/19.

The sum of the voltages U1 and U2 on the dielectric layers is equal to the source voltage U: U = U1 + U2; 10000 = U1 + U2.

Since U1 = 4/19 ∙ U2, then 10000 = 4/10 ∙ U2 + U2 = 23/19 ∙ U2; U2 = 190,000 /23 = 8260 V; U1 = U-U2 = 1740V.

The strength of the electric field in mica is E2 ∙ 8260 / 3.8≈2174 V / cm.

Mica has an electrical strength of 80,000 V / mm and can withstand such a voltage.

The electric field strength in the electric cardboard is E1 = 1740 / 0.2 = 8700 V / mm.

Electrical cardboard will not withstand such a voltage, since its dielectric strength is only 8000 V / mm.

6. A voltage of 60,000 V is connected to two metal plates 2 cm apart. Determine the electric field strength in the air gap, as well as the electric field strength in the air and glass if there is glass in the gap inserts a plate with a thickness of 1 cm (Fig. 5).

Rice. 5.

If there is only air between the plates, the electric field strength in it is equal to: E = U / d = 60,000 /2 = 30,000 V / cm.

The field strength is close to the dielectric strength of air.If a glass plate 1 cm thick (glass dielectric constant ε2 = 7) is introduced into the gap, then E1 = U1 / d1 = U1 / 1 = U1; E2 = U2 / d2 = U2 / 1 = U2; E1 / E2 = ε2 / ε1 = 7/1 = U1 / U2;

U1 = 7 ∙ U2; U1 = 60,000-U2; 8 ∙ U2 = 60,000; U2 = 7500 V; E2 = U2 / d2 = 7500 V / cm.

The strength of the electric field in the glass is E2 = 7.5 kV / cm, and its electric strength is 150 kV / cm.

In this case, the glass has a 20-fold safety factor.

For the air gap we have: U1 = 60,000-7500 = 52500 V; E1 = U1 / d1 = 52500 V / cm.

In this case, the strength of the electric field in the air gap is greater than in the first one, without glass. After glass is inserted, the whole combination has less strength than air alone.

The risk of breakage also occurs when the thickness of the glass plate is equal to the gap between the conductive plates, i.e. 2 cm, as there will inevitably be thin air gaps in the gap that will be punctured.

The dielectric strength of the gap between the high-voltage conductors must be reinforced with materials that have a low dielectric constant and a high dielectric strength, for example, electrical cardboard with ε = 2. Avoid combinations of materials with a high dielectric constant (glass, porcelain) and air, which must be replaced with oil.