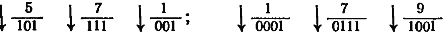Number systems
 A number system is a set of rules for representing numbers using different numerical signs. Number systems are classified into two types: non-positional and positional.
A number system is a set of rules for representing numbers using different numerical signs. Number systems are classified into two types: non-positional and positional.
In positional number systems, the value of each digit does not depend on the position it occupies, that is, on the place it occupies in the set of digits. In the Roman numeral system, there are only seven digits: one (I), five (V), ten (X), fifty (L), one hundred (C), five hundred (D), one thousand (M). Using these numbers (symbols), the remaining numbers are written by addition and subtraction. For example, IV is the notation of the number 4 (V — I), VI is the number 6 (V + I), and so on. The number 666 is written in the Roman system as follows: DCLXVI.
This notation is less convenient than the one we currently use. Here six is written with one symbol (VI), six tens with another (LX), six hundred and third (DC). It is very difficult to perform arithmetic operations with numbers written in the Roman numeral system. Also, a common drawback of non-positional systems is the complexity of representing large enough numbers in them so as to result in extremely cumbersome notation.
Now consider the same number 666 in the positional number system. In it, a single sign 6 means the number of ones if it is in the last place, the number of tens if it is in the penultimate place, and the number of hundreds if it is in the third place from the end. This principle of writing numbers is called positional (local). In such a recording, each digit receives a numerical value depending not only on its style, but also on where it stands when the number is written.
In the positional number system, any number represented as A = +a1a2a3 … ann-1an can be represented as a sum
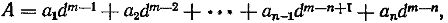
where n — finite number of digits in the image of a number, ii number i-go digit, d — base of the number system, i — ordinal number of the category, dm-i — "weight" of the i-ro category. Digits ai must satisfy the inequality 0 <= a <= (d — 1).
For decimal notation, d = 10 and ai = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Since numbers consisting of ones and zeros can be perceived as decimal or binary numbers when used together, the base of the number system is usually indicated, for example (1100)2-binary, (1100)10-decimal.
In digital computers, systems other than decimal are widely used: binary, octal, and hexadecimal.
Binary system
For this system d = 2 and here only two digits are allowed, i.e. ai = 0 or 1.
Any number expressed in the binary system is represented as the sum of the product of the power of base two times the binary digit of the given bit. For example, the number 101.01 can be written like this: 101.01 = 1×22 + 0x21 + 1×20 + 0x2-1 + 1×2-2, which corresponds to the number in the decimal system: 4 + 1 + 0.25 = 5.25 .
In most modern digital computers, the binary number system is used to represent numbers in a machine and perform arithmetic operations on them.
The binary number system, compared to the decimal one, makes it possible to simplify the circuits and circuits of the arithmetic device and the memory device and to increase the reliability of the computer. The digit of each bit of a binary number is represented by the «on / off» states of such elements as transistors, diodes, which work reliably in the «on / off» states. The disadvantages of the binary system include the need to translate according to a special program the original digital data into the binary number system and the results of the decision into decimal.
Octal number system
This system has base d == 8. Numbers are used to represent numbers: 0, 1, 2, 3, 4, 5, 6, 7.
The octal number system is used in the computer as an aid in preparing problems for solving (in the programming process), in checking the operation of a machine, and in debugging a program. This system gives a shorter representation of the number than the binary system. The octal number system allows you to simply switch to the binary system.
Hexadecimal number system
This system has base d = 16. 16 characters are used to represent numbers: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, and the characters A … F represent the decimal numbers 10, 11, 12, 13, 14 and 15. The hexadecimal number (1D4F) 18 will correspond to the decimal 7503 because (1D4F)18 = 1 x163 + 13 x 162 + 14 x 161+ 15 x 16O = (7503)10
Hexadecimal notation allows binary numbers to be written more compactly than octal. It finds application in input and output devices and number order display devices of some computers.
Binary-decimal number system
The representation of numbers in binary-decimal system is as follows. The decimal notation of the number is taken as a basis, and then each of its digits (from 0 to 9) is written in the form of a four-digit binary number called a tetrad, that is, not one sign is used to represent each digit of the decimal system, but four.
For example, the decimal 647.59 would correspond to BCD 0110 0100 0111, 0101 1001.
The binary-decimal number system is used as an intermediate number system and for encoding input and output numbers.
Rules for transferring one number system to another
The exchange of information between computer devices is carried out mainly through numbers represented in the binary number system. However, information is presented to the user in numbers in the decimal system, and command addressing is presented in the octal system. Hence the need to transfer numbers from one system to another in the process of working with a computer. To do this, use the following general rule.
To convert a whole number from any number system to another, it is necessary to successively divide this number by the base of the new system until the quotient is not less than the divisor. The number in the new system must be written in the form of remainders of division, starting with the last one, that is, from right to left.
For example, let's convert the decimal 1987 to binary:
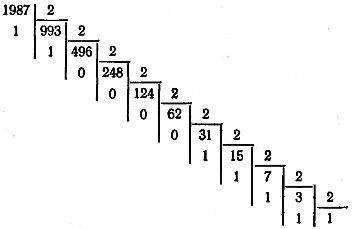
The decimal number 1987 in binary format is 11111000011, i.e. (1987)10 = (11111000011)2
When changing from any system to decimal, the number is represented as the sum of the powers of the base with the corresponding coefficients, and then the value of the sum is calculated.
For example, let's convert octal number 123 to decimal: (123)8 = 1 x 82 + 2 x 81 + 3 x 80 = 64 + 16 + 3 = 83, i.e. (123)8 = (83)10
To transfer the fractional part of a number from any system to another, it is necessary to carry out successive multiplication of this fraction and the resulting fractional parts of the product based on the new number system. The fractional part of a number in the new system is formed in the form of whole parts of the resulting products, starting from the first. The multiplication process continues until a number with a given precision is calculated.
For example, let's convert the decimal fraction 0.65625 to the binary number system:

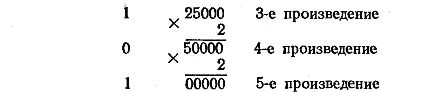
Since the fractional part of the fifth product consists only of zeros, further multiplication is unnecessary. This means that the given decimal is converted to binary without error, i.e. (0.65625)10 = (0.10101)2.
Converting from octal and hexadecimal to binary and vice versa is not difficult. This is because their bases (d — 8 and d — 16) correspond to integers of two (23 = 8 and 24 = 16).
To convert octal or hexadecimal numbers to binary, it is enough to replace each of their numbers with a three- or four-digit binary number, respectively.
For example, let's translate the octal number (571)8 and the hexadecimal number (179)16 to the binary number system.
In both cases we get the same result, i.e. (571)8 = (179)16 = (101111001)2
To convert a number from binary-decimal to decimal, you need to replace each tetrad of the number represented in binary-decimal with a digit represented in decimal.
For example, let's write the number (0010 0001 1000, 0110 0001 0110)2-10 in decimal notation, i.e. (0010 0001 1000, 0110 0001 0110)2-10 = (218,625)