What is an electrical supply?

Modern man constantly encounters electricity in everyday life and at work, uses devices that consume electric current and devices that generate it. When working with them, you should always take into account their capabilities inherent in the technical characteristics.

One of the main indicators of any electrical device is such a physical quantity as electrical energy... It is customary to call the intensity or speed of generation, transmission or conversion of electricity into other types of energy, for example, heat, light, mechanical.

The transportation or transfer of large electrical energy for industrial purposes is carried out according to high voltage power lines.

Transformation electrical energy is carried out at transformer substations.

Electricity consumption occurs in household and industrial devices for various purposes. One of their common types are incandescent lamps of various ratings.

The electrical power of generators, power lines and consumers in DC and AC circuits has the same physical meaning, which is simultaneously expressed in different ratios depending on the shape of the composite signals. To define the general patterns, notions of instantaneous values... They again emphasize the dependence of the rate of transformation of electricity on time.

Determination of instantaneous electrical power

In theoretical electrical engineering, in order to derive the basic relationships between current, voltage and power, their images in the form of instantaneous values, which are fixed at a certain point in time, are used.

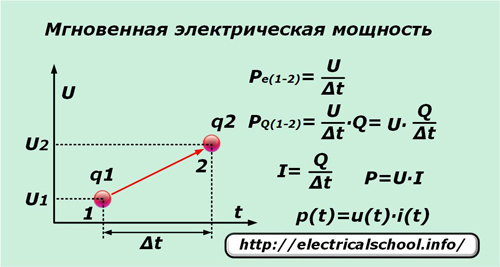
If in a very short period of time ∆t a single elementary charge q under the influence of voltage U moves from point «1» to point «2», then it performs work equal to the potential difference between these points. Dividing it by the time interval ∆t, we get the expression for the instantaneous power per unit charge Pe (1-2).

Since not only the single charge moves under the action of the applied voltage, but also all the adjacent ones that are under the influence of this force, the number of which is conveniently represented by the number Q, then the instantaneous value of the power PQ (1-2) can be written for them.

After performing simple transformations, we obtain the expression for the power P and the dependence of its instantaneous value p (t) on the components of the product of the instantaneous current i (t) and voltage u (t).

Determination of constant electrical power

V DC circuits the magnitude of the voltage drop in the circuit section and the current flowing through it does not change and remains stable, equal to the instantaneous values.Therefore, the power in this circuit can be determined by multiplying these values ​​or dividing the perfect work A by the period of its execution, as shown in the explanatory picture.

Determination of alternating current electrical power

The laws of sinusoidal variation of currents and voltages transmitted through electrical networks impose their influence on the expression of power in such circuits. Apparent power comes into play here, which is described by the power triangle and consists of active and reactive components.

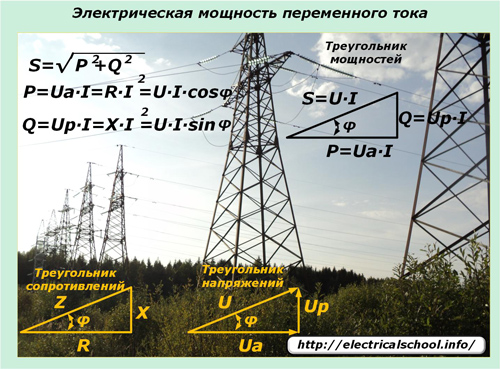
A sinusoidal electric current when passing through power lines with mixed types of loads in all sections does not change the shape of its harmonic. And the voltage drop at reactive loads shifts in phase in a certain direction. Moment value expressions help to understand the effect of applied loads on the power change in the circuit and its direction.

At the same time, immediately pay attention to the fact that the direction of the current flow from the generator to the consumer and the transmitted power through the created circuit are completely different things, which in some cases may not only not coincide, but also be directed in opposite directions.

Consider these relationships in their ideal, pure manifestation for different types of loads:

• active;

• capacitive;

• inductive.

Active load power dissipation

We will assume that the generator produces an ideal sinusoidal voltage u which is applied to the purely active resistance of the circuit. Ammeter A and voltmeter V measure current I and voltage U each time t.

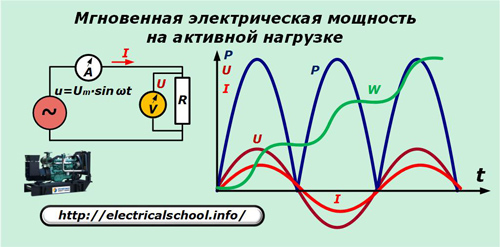
The graph shows that the sinusoids of the current and the voltage drop across the active resistance match in frequency and phase, making the same oscillations. The force expressed by their product oscillates at twice the frequency and always remains positive.

p = u ∙ i = Um ∙ sinωt ∙ Um / R ∙ sinωt = Um2/ R ∙ sin2ωt = Um2/ 2R ∙ (1-cos2ωt).

If we go to the expression operating voltage, then we get: p = P ∙ (1-cos2ωt).

We will then integrate the power over the period of one oscillation T and we will be able to notice that the energy gain ∆W during this interval increases. Over time, the resistance continues to consume new portions of electricity, as shown in the graph.

With reactive loads, the characteristics of energy consumption are different, they have a different shape.

Capacitive power dissipation

In the electrical circuit of the generator, replace the resistive element with a capacitor of capacitance C.

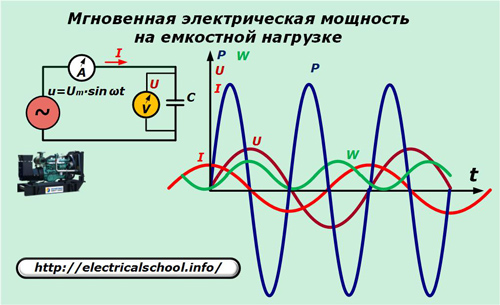
The relationship between the current and the voltage drop in the capacitance is expressed by the ratio: I = C ∙ dU / dt = ω ∙ C ∙ Um ∙ cosωt.

We multiply the values ​​​​of the instantaneous expressions of current with voltage and get the value of the power that is consumed by the capacitive load.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Um ∙ cosωt = ω ∙ C ∙ Um2∙ sinωt ∙ cosωt = Um2/ (2X° C) ∙ sin2ωt = U2/ (2X° C) ∙ sin2ωt.

Here you can see that the power fluctuates around zero at twice the frequency of the applied voltage. Its total value for the harmonic period, as well as the energy gain, is zero.

This means that energy moves along the closed circuit of the circuit in both directions, but does no work.Such a fact is explained by the fact that when the source voltage increases in absolute value, the power is positive, and the energy flow through the circuit is directed to the container, where energy is accumulated.

After the voltage passes to the falling harmonic section, energy is returned from the capacitor to the circuit to the source. No useful work is done in either process.

Power dissipation in an inductive load

Now, in the supply circuit, replace the capacitor with inductance L.

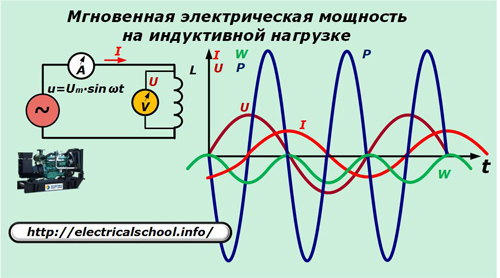
Here the current through the inductance is expressed by the ratio:

I = 1 / L∫udt = -Um / ωL ∙ cos ωt.

Then we get

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ (-Um / ωL ∙ cosωt) = — Um2/ ωL ∙ sinωt ∙ cosωt = -Um2/ (2ХL) ∙ sin2ωt = -U2/ (2ХL) ∙ sin2ωt.

The resulting expressions allow us to see the nature of the change in the direction of the power and the increase of energy on the inductance, which perform the same oscillations that are useless for doing work, as on the capacitance.

The power released in reactive loads is called reactive component. In ideal conditions, when the connecting wires have no active resistance, it appears harmless and does not cause any harm. But in real power conditions, periodic transients and reactive power fluctuations cause heating of all active elements, including connecting wires, for which some energy is consumed and the value of the applied full power of the source decreases.

The main difference between the reactive component of power is that it does not perform useful work at all, but leads to losses of electrical energy and excess loads on equipment, which are especially dangerous in critical situations.

For these reasons, to eliminate the influence of reactive power, esp technical systems for its compensation.

Power distribution at mixed load

As an example, we use the load of a generator with an active capacitive characteristic.

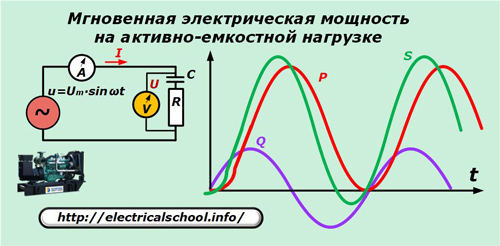
To simplify the picture, the sinusoids of currents and voltages are not shown in the given graph, but it should be borne in mind that with an active-capacitive nature of the load, the current vector leads the voltage.

p = u ∙ i = Um ∙ sinωt ∙ ωC ∙ Im ∙ sin (ωt + φ).

After transformations we get: p = P ∙ (1- cos 2ωt) + Q ∙ sin2ωt.

These two terms in the last expression are the active and reactive components of the instantaneous apparent power. Only the first of these does useful work.

Power measurement tools

To analyze the consumption of electricity and calculate for it, measuring devices are used, which have long been called «Counters»… Their work is based on measuring the effective values ​​​​of current and voltage and automatically multiplying them with an output of information.

Meters display energy consumption by counting the operating time of electrical appliances on an incremental basis from the moment the meter is switched on under load.

To measure the active component of power in AC circuits, wattmeters, and reactive - varmeters. They have different unit designations:

• watt (W, W);

• var (var, var, var).

To determine the total energy consumption, it is necessary to calculate its value using the power triangle formula based on the readings of the wattmeter and varmeter. It is expressed in its own units — volt-amperes.

The accepted designations of the units of each help electricians to judge not only its value, but also the nature of the power component.