Temperature coefficient of resistance

The electrical resistance of a conductor usually depends on the material of the conductor, on its length and cross-section, or, more briefly, on the resistance and on the geometrical dimensions of the conductor. This dependence is well known and is expressed by the formula:

Known to all and Ohm's law for a homogeneous section of an electric circuit, from which it can be seen that the higher the resistance, the lower the current. Thus, if the resistance of the wire is constant, then as the applied voltage increases, the current should increase linearly. But in reality this is not the case. The resistance of wires is not constant.

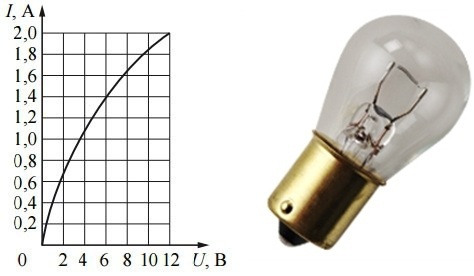
You don't have to go far for examples. If you connect a light bulb to an adjustable power supply (with a voltmeter and an ammeter) and gradually increase the voltage on it, bringing it to the nominal value, you will easily see that the current does not grow linearly: the voltage approaches the nominal value of the lamp, the current through its coil grows more and more slowly and the light becomes more and more bright.

There is no such thing as doubling the voltage applied to the coil will double the current. Ohm's law does not seem to hold. In fact, Ohm's law is fulfilled and exactly the resistance of the filament of the lamp is not constant, it depends on the temperature.

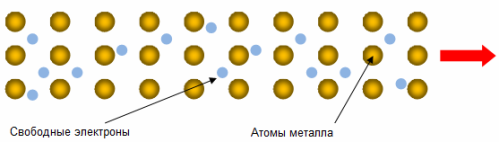
Let's recall what is the reason for the high electrical conductivity of metals. It is associated with the presence in metals of a large number of charge carriers — current components — conduction electrons… These are electrons formed by the valence electrons of the metal atoms, which are common to the entire conductor, they do not belong to each individual atom.

Under the action of an electric field applied to the conductor, the free conduction electrons go from chaotic to more or less ordered movement — an electric current is formed. But the electrons encounter obstacles on their way, inhomogeneities of the ion lattice, such as lattice defects, an inhomogeneous structure caused by its thermal vibrations.

Electrons interact with ions, lose momentum, their energy is transferred to the lattice ions, transformed into lattice ion vibrations, and the chaos of the thermal movement of the electrons themselves increases, from which the conductor heats up when the current passes through it.

In dielectrics, semiconductors, electrolytes, gases, nonpolar liquids—the reason for the resistance may be different, but Ohm's law obviously does not remain permanently linear.

Thus, for metals, an increase in temperature leads to an even greater increase in the thermal vibrations of the crystal lattice, and the resistance to the movement of conduction electrons increases.This can be seen from the experiment with the lamp: the brightness of the glow increases, but the current increases less. This means that the change in temperature affected the resistance of the lamp filament.

As a result, it becomes clear that the resistance metal wires depends almost linearly on temperature. And if we take into account that when heated, the geometric dimensions of the wire slightly change, then the electrical resistance also depends almost linearly on the temperature. These dependencies can be expressed by the formulas:

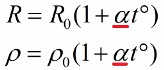
Let's pay attention to the odds. Suppose that at 0 ° C the resistance of the conductor is R0, then at a temperature t ° C it will take the value R (t), and the relative change in resistance will be equal to α * t ° C. This proportionality factor α is called the temperature coefficient of resistance... It characterizes the dependence of the electrical resistance of the substance on its current temperature.

This coefficient is numerically equal to the relative change in electrical resistance of a conductor when its temperature changes by 1K (one degree Kelvin, which is equivalent to a one degree Celsius change in temperature).

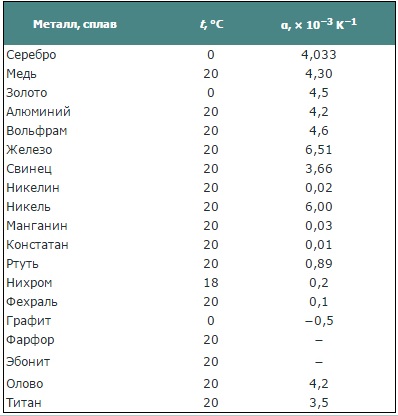
For metals, TCR (temperature coefficient of resistance α), although relatively small, is always greater than zero, because when the current passes, electrons more often collide with ions of the crystal lattice, the higher the temperature, t .is the higher their thermal chaotic motion and the higher their speed.Colliding in chaotic motion with lattice ions, the electrons of the metal lose energy, which we see as a result — the resistance increases as the wire heats up. This phenomenon is used technically in resistance thermometers.

Thus, the temperature coefficient of resistance α characterizes the dependence of the electrical resistance of the substance on temperature and is measured in 1 / K — kelvin to the power of -1. The value with the opposite sign is called the temperature coefficient of conductivity.

As for pure semiconductors, TCS is negative for them, that is, the resistance decreases with increasing temperature, this is due to the fact that as the temperature increases, more and more electrons pass into the conduction zone, while the concentration of holes also increases. The same mechanism is characteristic of liquid nonpolar and solid dielectrics.

Polar liquids sharply decrease their resistance with increasing temperature due to a decrease in viscosity and an increase in dissociation. This property is used to protect electron tubes from the destructive effects of high inrush currents.

For alloys, doped semiconductors, gases and electrolytes, the thermal dependence of resistance is more complex than for pure metals. Alloys with very low TCS, such as manganin and constantan, are used in electrical measuring instruments.