Electrical resistance of wires

The concept of electrical resistance and conductivity

Any body through which an electric current flows has a certain resistance to it. The property of a conducting material to prevent an electric current from passing through it is called electrical resistance.

Electronic theory explains the nature of the electrical resistance of metallic conductors in this way. Free electrons, when moving along a wire, encounter atoms and other electrons on their way countless times and, interacting with them, inevitably lose some of their energy. Electrons experience resistance to their motion anyway. Different metal conductors with different atomic structures have different resistance to electric current.

Exactly the same explains the resistance of liquid conductors and gases to the passage of electric current. However, we must not forget that in these substances, not electrons, but charged particles of molecules encounter resistance during their movement.

Resistance is denoted by the Latin letters R or r.

The ohm is taken as the unit of electrical resistance.

Ohm is the resistance of a column of mercury 106.3 cm high with a cross section of 1 mm2 at a temperature of 0 ° C.

If, for example, the electrical resistance of the wire is 4 ohms, then it is written like this: R = 4 ohms or r = 4 th.

For measuring resistances of large value, a unit called megohm is adopted.

One megohm equals one million ohms.

The greater the resistance of the wire, the worse it conducts electric current, and conversely, the lower the resistance of the wire, the easier it is for electric current to pass through this wire.

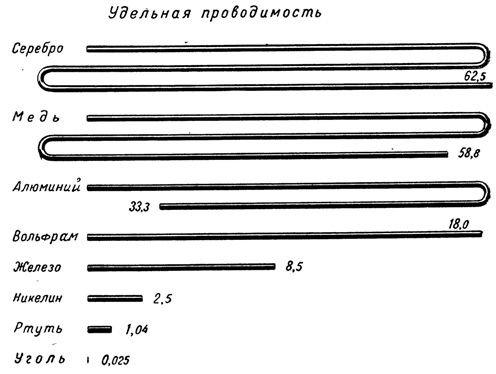
Therefore, for the characteristics of a conductor (from the point of view of the passage of an electric current through it), one can take into account not only its resistance, but also the value inverse of the resistance and called conductivity.

Electrical conductivity is called the ability of a material to pass an electric current through itself.

Since conductance is the reciprocal of resistance, it is expressed as 1 /R, conductance is denoted by the Latin letter g.

Influence of the material of the conductor, its dimensions and the ambient temperature on the value of electrical resistance

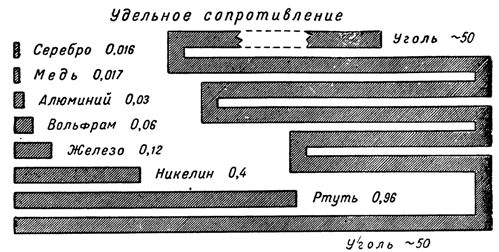
The resistance of different wires depends on the material they are made of. To characterize the electrical resistance of various materials, the concept of the so-called Resistance.

Resistance called the resistance of a wire with a length of 1 m and a cross-sectional area of ​​1 mm2. Resistance is denoted by the Greek letter p. Each material from which a conductor is made has its own specific resistance.

For example, the resistance of copper is 0.017, that is, a copper wire with a length of 1 m and a cross section of 1 mm2 has a resistance of 0.017 ohms. The resistance of aluminum is 0.03, the resistance of iron is 0.12, the resistance of constantan is 0.48, and the resistance of nichrome is 1-1.1.

Read more about it here: What is electrical resistance?

The resistance of a wire is directly proportional to its length, that is, the longer the wire, the greater its electrical resistance.

The resistance of a wire is inversely proportional to its cross-sectional area, that is, the thicker the wire, the lower its resistance, and conversely, the thinner the wire, the higher its resistance.

To better understand this relationship, imagine two pairs of communicating vessels, one pair of vessels having a thin connecting tube and the other a thick one. It is clear that when one of the vessels (each pair) is filled with water, its transfer to another vessel through a thick pipe will take place much faster than through a thin one, i.e. a thick pipe will have less resistance to the flow of water. Similarly, it is easier for an electric current to pass through a thick wire than through a thin one, that is, the former has less resistance than the latter.

The electrical resistance of a conductor is equal to the specific resistance of the material from which this conductor is made, multiplied by the length of the conductor and divided by the area of ​​​​the cross-sectional area of ​​​​the conductor:

R = p l / S,

where — R — resistance of the wire, ohm, l — length in the wire in m, C — cross-sectional area of ​​the wire, mm2.

Cross-sectional area of ​​a round wire calculated by the formula:

S = Pi xd2 / 4

where Pi is a constant value equal to 3.14; d — diameter of the wire.

And this is how the length of the wire is determined:

l = S R / p,

This formula makes it possible to determine the length of the wire, its cross-section and resistance, if the other quantities included in the formula are known.

If it is necessary to determine the cross-sectional area of ​​​​the wire, then the formula leads to the following form:

S = p l / R

Transforming the same formula and solving the equality in terms of p, we find the resistance of the wire:

R = R S / l

The latter formula should be used in cases where the resistance and dimensions of the conductor are known, but its material is unknown, and moreover it is difficult to determine from its appearance. To do this, it is necessary to determine the resistance of the wire and, using the table, find a material with such a resistance.

Another factor that affects the resistance of wires is temperature.

It has been established that with an increase in temperature, the resistance of metal wires increases, and with a decrease, it decreases. This increase or decrease in resistance for pure metal conductors is almost the same and averages 0.4% per 1 °C... The resistance of liquid conductors and coal decreases with increasing temperature.

The electronic theory of the structure of matter gives the following explanation for the increase in resistance of metal conductors with increasing temperature.When heated, the conductor receives thermal energy, which is inevitably transmitted to all atoms of the substance, as a result of which the intensity of their movement increases. The increased movement of atoms creates greater resistance to the directed movement of free electrons, which is why the resistance of the conductor increases. As the temperature decreases, better conditions are created for the directional movement of electrons and the resistance of the conductor decreases. This explains an interesting phenomenon — superconductivity of metals.

SuperconductivityReduction of the resistance of metals to zero occurs at a huge negative temperature -273° ° So-called absolute zero. At a temperature of absolute zero, metal atoms appear to freeze in place, completely undisturbed by the movement of electrons.