Resonance of currents

Parallel connection of a capacitor and an inductor in an alternating current circuit

Consider the phenomena in the circuit alternating currentcontaining a generator, capacitor and inductor connected in parallel. Assume that the circuit has no active resistance.

Obviously, in such a circuit the voltage of both the coil and the capacitor at any time is equal to the voltage developed by the generator.

The total current in a circuit consists of the currents in its branches. The current in the inductive branch lags the voltage in phase by a quarter of the period, and the current in the capacitive branch leads it by the same quarter of the period. Therefore, the currents in the branches at any instant of time turn out to be phase-shifted relative to each other by half a period, that is, they are in antiphase. Thus, the currents in the branches at any time are directed towards each other, and the total current in the unbranched part of the circuit is equal to their difference.

This gives us the right to write equality I = IL -integral circuit

where I— effective value of the total current in the circuit, I L and integrated circuit — effective values ​​of currents in the branches.

Using Ohm's law to determine the effective values ​​of the current in the branches, we get:

Il = U / XL and Az° C = U / XC

If the circuit is dominated by inductive resistance, ie. XL More ▼ XC, the current in the coil is less than the current in the capacitor; therefore the current in the unbranched section of the circuit is capacitive in nature and the circuit as a whole for the generator will be capacitive. Conversely, with XC greater than XL, the current in the capacitor is less than the current in the coil; therefore the current in the unbranched section of the circuit is inductive, and the circuit as a whole for the generator will be inductive.

It should not be forgotten that in both cases the load is reactive, i.e. the circuit does not consume the power of the generator.

Resonance of currents

Let us now consider the case when the capacitor and coil connected in parallel turned out to be equal in their reactance, i.e. XlL = X°C.

If, as before, we assume that the coil and the capacitor have no active resistance, then if their reactions are equal (YL = Y° C) the total current in the unbranched part of the circuit will be zero, while in the branches equal currents will flow with greatest magnitude. In this case, the phenomenon of resonance currents occurs in the circuit.

At current resonance, the effective values ​​of the currents in each branch, determined by the ratios IL = U / XL and Аz° С = U / XC will be equal to each other, so that XL = XC.

The conclusion we reached may seem rather strange at first glance. In fact, the generator is loaded with two resistances and there is no current in the unbranched part of the circuit, while equal and, moreover, the largest currents flow in the resistances themselves.

This is explained by the behavior of the magnetic field of the coil and electric field of a capacitor… At resonance of currents, as in voltage resonance, there is an energy fluctuation between the field of the coil and the field of the capacitor. The generator, after communicating the energy to the circuit, appears to be isolated. It can be turned off completely and the current in the branched part of the circuit will be maintained without a generator by the energy that the circuit initially stores. Also, the voltage across the circuit terminals will remain exactly the same as that developed by the generator.

Thus, when the inductor and the capacitor are connected in parallel, we obtained an oscillator circuit that differs from the one described above only in that the generator that creates the oscillations is not connected directly to the circuit and the circuit is closed. 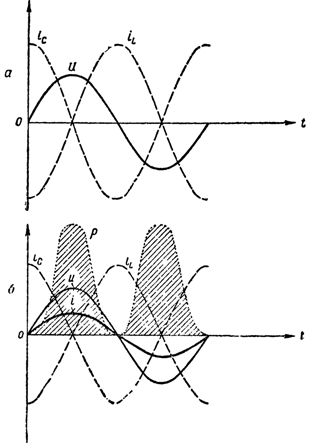Graphs of currents, voltage and power in the circuit at resonance of currents: a — the active resistance is equal to zero, the circuit does not consume energy; b — the circuit has an active resistance, a current has appeared in the unbranched part of the circuit, the circuit consumes energy

L, C and e, at which current resonance occurs, are determined, as in voltage resonance (if we neglect the active resistance of the circuit), by the equality:

ωL = 1 / ω° C

Therefore:

eres = 1 / 2π√LC

Lres = 1 / ω2C

Piece = 1 / ω2L

By changing any of these three quantities, the equality Xl = X° C can be achieved, i.e., turn the circuit into an oscillating circuit.

So, we have a closed oscillating circuit in which we can induce electrical oscillations, i.e. alternating current. And if it were not for the active resistance which every oscillating circuit possesses, an alternating current might continuously exist in it.The presence of active resistance leads to the fact that the oscillations in the circuit gradually die down, and to maintain them, an energy source is needed - an alternator.

In non-sinusoidal current circuits, resonant modes are possible for various harmonic components.

Resonant currents are widely used in practice. The phenomenon of current resonance is used in bandpass filters as an electrical "clamp" that delays a certain frequency. Since there is a significant current resistance at frequency f, the voltage drop in the circuit at frequency f will be maximum. This property of the loop is called selectivity, it is used in radio receivers to isolate the signal of a particular radio station. An oscillating circuit operating in a resonant mode of currents is one of the main components electronic generators.