Complex alternating currents

In addition to the simple ones, ie. sinusoidal alternating currentscomplex currents are often encountered, in which the graph of the current change over time is not a sinusoid, but a more complex curve. In other words, for such currents the law of variation of the current with time is more complicated than for a simple sinusoidal current. An example of such a current is shown in fig. 1.

The study of these currents is based on the fact that any complex non-sinusoidal current can be considered as consisting of several simple sinusoidal currents, the amplitudes of which are different, and the frequencies are a whole number of times greater than the frequency of a given complex current. Such a decomposition of a complex current into a series of simple currents is important, because in many cases the study of a complex current can be reduced to the consideration of simple currents for which all the basic laws have been derived in electrical engineering.

Rice. 1. Complex non-sinusoidal current

They are called simple sinusoidal currents that form complex current harmonics and are numbered in ascending order of their frequency.For example, if a complex current has a frequency of 50 Hz, then its first harmonic, otherwise called the fundamental oscillation, is a sinusoidal current with a frequency of 50 Hz, the second harmonic is a sinusoidal current with a frequency of 100 Hz, the third harmonic has a frequency of 150 Hz, and so on.

A harmonic number indicates how many times its frequency is greater than the frequency of a given complex current. As the number of harmonics increases, their amplitudes usually decrease, but there are exceptions to this rule. Sometimes some harmonics are completely absent, that is, their amplitudes are equal to zero. Only the first harmonic is always present.

Rice. 2. Complex alternating current and its harmonics

As an example, FIG. 2a shows a plot of complex current consisting of the first and second harmonics and plots of these harmonics, and in FIG. 2, b, the same is shown for the current consisting of the first and third harmonics. In these graphs, adding harmonics and obtaining the total current with a complex shape is done by adding vertical segments depicting currents at different times, taking into account their signs (plus and minus).

Sometimes a complex current, in addition to harmonics, also includes D.C., that is, a constant component. Since the constant frequency is zero, the constant component can be called the zeroth harmonic.

It is difficult to find the harmonics of a complex current. A special section of mathematics called harmonic analysis is devoted to this... However, according to some signs, the presence of certain harmonics can be judged. For example, if the positive and negative half-waves of a complex current are the same in shape and maximum value, then such a current contains only one odd harmonic.

An example of such a current is given in fig. 2, b.If the positive and negative half-waves differ from each other in shape and maximum value (Fig. 2, a), this serves as a sign of the presence of even harmonics (in this case, there may also be odd harmonics).

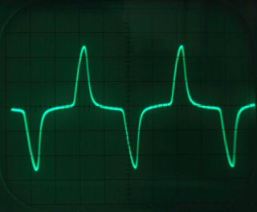
Rice. 3. Complex alternating current on the oscilloscope screen

Alternating voltages and complex-shaped EMFs, such as complex currents, can be represented as a sum of simple sinusoidal components.

Regarding the physical meaning of the decomposition of complex currents into harmonics, what has been said can be repeated pulsating current, which should also be classified as complex currents.

In electric circuits consisting of linear devices, the action of a complex current can always be considered and calculated as the total action of its component currents. However, in the presence of non-linear devices, this method has a more limited application, since it can give significant errors when solving a number of problems.

See also on this topic: Calculation of non-sinusoidal current circuits