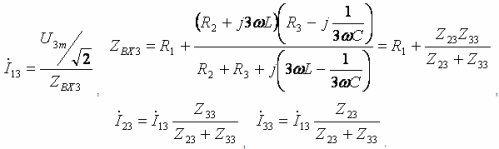Electric circuits with non-sinusoidal current
Non-sinusoidal currents and their decomposition
In an electrical circuit, non-sinusoidal currents can occur for two reasons:
-
the electric circuit itself is linear, but a non-sinusoidal voltage acts on the circuit,
-
the voltage acting on the circuit is sinusoidal, but the electrical circuit contains non-linear elements.
There could be both reasons. This chapter deals with circuits for the first point only. In this case, the non-sinusoidal voltages are considered to be periodic.
Generators of periodic pulses are used in various devices of radio engineering, automation, telemechanics. The shape of the pulses can be different: saw, stepped, rectangular (Fig. 1).
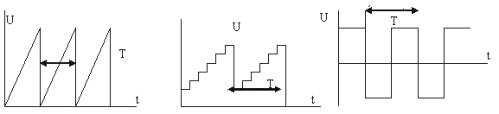
Figure 1. Pulse shapes
The phenomena occurring in a linear electrical circuit under periodic but non-sinusoidal voltages are easiest to study if the voltage curve is expanded in a trigonometric Fourier series:
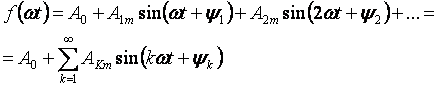
The first term of the series A0 is called the constant component or zeroth harmonic, the second term of the series
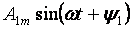
— the fundamental or first harmonic and all other members of the form
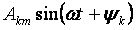
for k> 1 are called higher harmonics.
If in expression (3.1) we open the sine of the sum, then we can move to another form of writing the series:
If the function is symmetric about the abscissa axis, then the series does not contain a constant component. If the function is symmetric about the ordinate axis, then the series contains no sines. The function is symmetric about the origin and contains no cosines.
Some examples of series expansion are given in a table. 1 and they are also available in the reference literature.
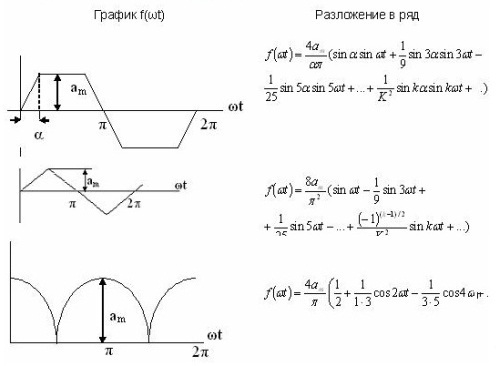
Table 1. Fourier series expansion
Calculation of non-sinusoidal current circuits
The circuit is calculated for each harmonic according to the model. The circuit is calculated as many times as there are harmonics in the voltage acting on the circuit. In this case, it is necessary to take into account a number of characteristics.
It should be noted that the resistance of the inductive element increases as the harmonic number increases
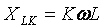
and the capacitive element, on the contrary, decreases:
It should also be taken into account that the constant component of the current does not pass through the capacitor and the inductance is not a resistance to it.
In addition, one should not forget the possible resonance phenomena not only at the fundamental harmonic, but also at higher harmonics.
Vector diagrams can be plotted for each harmonic separately.
According to the principle of superposition, the current of each branch can consist of the sum of individual terms (zero, fundamental and higher harmonics):
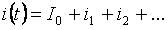
The rms value of the total branch current can be determined by the average value of the individual harmonic currents:
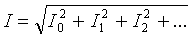
The active power of the non-sinusoidal current is equal to the sum of the active powers of the individual harmonics:
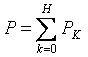
Below is a general example for calculating non-sinusoidal current circuits. All currents, voltages, resistances will have two indices: the first digit means the branch number and the second digit the harmonic number. Input voltage:
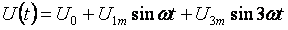
- Permanent component
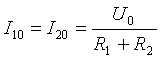
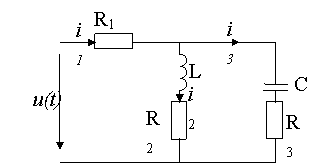
Figure 2. Electrical diagram
- Major Harmonic:
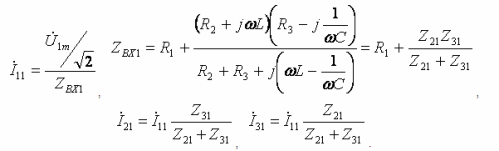
- Third harmonic:
