Power balance in an electrical circuit
According to The Joule-Lenz law work done by a direct current in a resistance,

If another converter of electromagnetic energy into mechanical or chemical or other form of energy (electric motor, charging battery, etc.) is included in the considered branch instead of a resistor, the work done by the current during the time t can be calculated in the case that if the converter voltage is known.
In this case, the Joule-Lenz formula takes a different form:
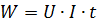
At direct current, the power supplied to the section of the circuit with resistance r is given by the expression:
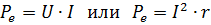
where I, U and r retain the same meaning as in the Joule-Lenz formula.
The power consumed in the entire external circuit and the power supplied by the generator are the same. The power developed by the generator is always greater than that which the generator gives to the external circuit, because part of the power is spent to cover losses inside the generator itself.
A power balance expression for a single closed loop containing a generator with emf E and internal resistance ri and a resistor of resistance r can be obtained from the Kirchhoff equation.
For this circuit

If both sides of this equation are multiplied by the current in the circuit, then the resulting equation will represent the power balance in that circuit
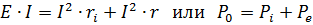
The power developed by the generator is equal to the sum of the power lost inside the generator and given to the external circuit. P0 = EI is the power developed by the generator, Pe = UI = I2r is the power that the generator gives to the external circuit, and Pi — I2ri is the power lost inside the generator itself.
When choosing the same positive directions of the current through the double-ended terminal I and the voltage of the double-ended terminal U, the power consumed by the two terminals, that is, the user interface of the product, must be positive. If at the same time it turns out that the user interface of the product is negative, this will mean that the device with two terminals does not consume electromagnetic energy, but on the contrary, it is a generator of electromagnetic energy and gives this energy to electrical circuit.
If in an electrical circuit a number of devices with two terminals emit electromagnetic energy to the circuit, the others absorb this energy. In a direct current circuit, no accumulation of electromagnetic energy can occur. Therefore, the sum of the power consumed in passive two-terminal networks and the power lost inside the generators must be equal to the algebraic sum of the powers developed by all generators, i.e. the sum of the products EkIk of all generators working in a circuit:
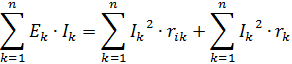
where n — the number of branches in the chain.
The balance equation obtained for a simple circuit containing one generator can be rewritten by expressing the power consumed in the external circuit as the power expressed by the generator and the power lost inside the generator:


