Law of conservation of energy

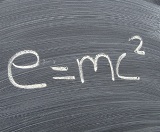Modern physics knows many types of energy associated with motion or different mutual arrangement of a wide variety of material bodies or particles, for example, any moving body has kinetic energy proportional to the square of its velocity. This energy can change if the speed of the body increases or decreases. A body raised above the ground has a gravitational potential energy varying three changes in the height of the body.

Stationary electric charges that are some distance from each other have an electrostatic potential energy in accordance with the fact that, according to Coulomb's law, the charges either attract (if they are of different signs) or repel with a force inversely proportional to the square of the distance between them.

Kinetic and potential energy is possessed by molecules, atoms and particles, their constituents — electrons, protons, neutrons, etc. in the form of mechanical work, in the flow of electric current, in the transfer of heat, in the change of the internal state of bodies, in the propagation of electromagnetic waves, etc.

More than 100 years ago, a fundamental law of physics was established, according to which energy cannot disappear or arise from nothing. She can only change from one type to another…. This law is called the law of conservation of energy.

In the works of A. Einstein, this law is significantly developed. Einstein established the interchangeability of energy and mass and thereby expanded the interpretation of the law of conservation of energy, which is now commonly stated as the law of conservation of energy and mass.

In accordance with Einstein's theory, any change in the body's energy dE is related to a change in its mass dm by the formula dE =dmc2, where c is the speed of light in a vacuum equal to 3 x 108 Miss.

From this formula, in particular, it follows that if, as a result of some process, the mass of all bodies involved in the process decreases by 1 g, then the energy equal to 9×1013 J, which is equivalent to 3000 tons of standard fuel.

These ratios are of primary importance in the analysis of nuclear transformations. In most macroscopic processes, the change in mass can be neglected and only the law of conservation of energy can be spoken of.

Let us trace the transformations of energy on some concrete example. Consider the entire chain of energy conversions required to produce any part on a lathe (Fig. 1). Let the initial energy 1, the amount of which we take as 100%, is obtained due to the complete combustion of a certain amount of fossil fuel. Therefore, for our example, 100% of the initial energy is contained in the products of fuel combustion, which are at a high (about 2000 K) temperature.

The products of combustion in the boiler of the power plant, when cooled, give up their internal energy in the form of heat to water and water vapor. However, for technical and economic reasons, the combustion products cannot be cooled to ambient temperature. They are ejected through the tube into the atmosphere at a temperature of about 400 K, taking with them some of the original energy. Therefore, only 95% of the initial energy will be transferred to the internal energy of the water vapor.

The resulting water vapor will enter the steam turbine, where its internal energy is initially partially converted into kinetic energy of the steam strings, which will then be transmitted as mechanical energy to the turbine rotor.

Only part of the steam energy can be converted into mechanical energy. The rest is given to the cooling water when steam is condensed in the condenser. In our example, we assumed that the energy transferred to the turbine rotor would be about 38%, which roughly corresponds to the state of affairs in modern power plants.

When converting mechanical energy into electrical energy due to the so-called Joule losses in the rotor and stator windings of the generator will lose about 2% of the energy. As a result, about 36% of the initial energy will go into the grid.

An electric motor will convert only a portion of the electrical energy supplied to it into mechanical energy to rotate the lathe. In our example, about 9% of the energy in the form of Joule heat in the motor windings and frictional heat in its bearings will be released into the surrounding atmosphere.

Thus, only 27% of the initial energy will be delivered to the working organs of the machine. But the energy mishaps don't end there either. It turns out that most of the energy during the machining of a part is spent on friction and in the form of heat is removed with the liquid that cools the part. Theoretically, only a very small fraction (in our example, 2% is assumed) of the initial energy would be sufficient to obtain the desired part of the original part.

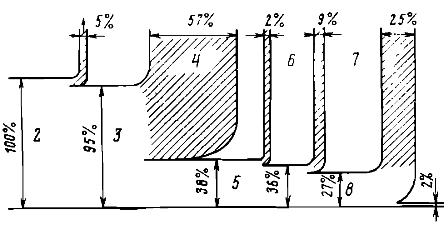
Rice. 1. Diagram of energy transformations during processing of a workpiece on a lathe: 1 — energy loss with exhaust gases, 2 — internal energy of combustion products, 3 — internal energy of the working fluid — water vapor, 4 — heat released from the cooling water in a turbine condenser, 5 — mechanical energy of the rotor of a turbine generator, 6 — losses in the electric generator, 7 — waste in the electrical drive of the machine, 8 — mechanical energy of rotation of the machine, 9 — frictional work, which is converted into heat, separated from the liquid, the cooling part, 10 — increasing the internal energy of the part and chips after processing ...

At least three very useful conclusions can be drawn from the example under consideration, if it is considered fairly typical.

First, at each step of the energy conversion some of it is lost... This statement should not be understood as a violation of the law of conservation of energy. It is lost because of the useful effect for which the corresponding transformation is performed. The total amount of energy after the conversion remains unchanged.

If the process of energy conversion and transfer takes place in a certain machine or apparatus, then the efficiency of this device is usually characterized by efficiency (efficiency)... A diagram of such a device is shown in fig. 2.

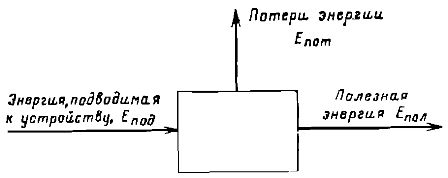
Rice. 2. Scheme for determining the efficiency of a device that converts energy.

Using the notation shown in the figure, the efficiency can be defined as Efficiency = Epol/Epod

It is clear that in this case, based on the law of conservation of energy, there must be Epod = Epol + Epot

Therefore, the efficiency can also be written as follows: efficiency = 1 — (Epot / Epol)

Returning to the example shown in FIG. 1, we can say that the efficiency of the boiler is 95%, the efficiency of converting the internal energy of steam into mechanical work is 40%, the efficiency of the electric generator is 95%, the efficiency is — the electric drive of a machine — 75%, and the efficiency of the actual processing of the workpiece is about 7%.

In the past, when the laws of energy transformation were not yet known, people's dream was to create a so-called perpetual motion machine — a device that would do useful work without spending energy. Such a hypothetical engine, the existence of which would violate the law of conservation of energy, is today called a perpetual motion machine of the first kind, as opposed to a perpetual motion machine of the second kind. Today, of course, no one takes seriously the possibility of creating a perpetual motion machine of the first kind.

Second, all energy losses are ultimately converted into heat, which is released either to atmospheric air or to water from natural reservoirs.

Third, people end up using only a small fraction of the primary energy that is expended to obtain the relevant beneficial effect.

This is particularly evident when looking at energy transport costs. In idealized mechanics, which does not consider frictional forces, moving loads in the horizontal plane require no energy.

In real conditions, all the energy consumed by a vehicle is used to overcome frictional forces and air resistance forces, that is, ultimately, all the energy consumed in transport is converted into heat. In this regard, the following figures are interesting, characterizing the work of moving 1 ton of cargo at a distance of 1 km with different types of transport: airplane — 7.6 kWh / (t-km), car — 0.51 kWh / ( t-km) , train-0.12 kWh / (t-km).

Thus, the same beneficial effect can be achieved with air transport at the expense of 60 times greater energy consumption than with rail. Of course, high energy consumption gives significant time savings, but even at the same speed (car and train), energy costs differ by 4 times.

This example suggests that people often make trade-offs with energy efficiency in order to achieve other goals, for example comfort, speed, etc. As a rule, the energy efficiency of the process itself is of little interest to us — the general technical and economic evaluations of the efficiency of processes is important... But as the price of primary energy components increases, the energy component in technical and economic evaluations becomes more and more important.