Laws of Contact Circuit Algebra, Boolean Algebra

An analytical record of the structure and operating conditions of relay circuits makes it possible to carry out analytical equivalent transformations of circuits, that is, by transforming structural formulas, finding schemes similar in their operation. Conversion methods are especially fully developed for structural formulas expressing contact circuits.

For contact circuits, the mathematical apparatus of the algebra of logic is used, more precisely, one of its simplest varieties, called proposition calculus or Boolean algebra (after the mathematician of the last century J. Boole).

The propositional calculus was originally developed to study the dependence (the truth or falsity of complex judgments on the truth or falsity of the simple propositions that compose them. In essence, the propositional calculus is an algebra of two numbers, that is, an algebra in which each individual argument and each function can have one of two values.

This determines the possibility of using Boolean algebra to transform contact circuits, since each of the arguments (contacts) included in the structural formula can take only two values, that is, it can be closed or open, and the entire function represented by the structural the formula can express either a closed or an open circuit.

Boolean algebra introduces:

1) objects that, as in ordinary algebra, have names: independent variables and functions — however, unlike ordinary algebra, in Boolean algebra both can take only two values: 0 and 1;

2) basic logic operations:

• logical addition (or disjunction, logical OR, denoted by the sign ?), which is defined as follows: the result of the operation is 0 if and only if all the arguments of the operation are equal to 0, otherwise the result is 1;

• logical multiplication (or concatenation, logical AND, denoted by ?, or not specified at all) which is defined as follows: the result of the operation is 1 if and only if all the arguments of the operation are equal to 1, otherwise the result is 0;

• negation (or vice versa, logical NOT, indicated by a bar above the argument), which is defined as follows: the result of the operation has the opposite value of the argument;

3) axioms (laws of Boolean algebra), which define the rules for transforming logical expressions.

Note that each of the logical operations can be performed both on variables and on functions, which will be called Boolean functions below... Recall that, by analogy with ordinary algebra, in Boolean algebra, the operation of logical multiplication has precedence over the logical addition operation.

Boolean expressions are formed by combining logical operations on a number of objects (variables or functions), called arguments of the operation.

The transformation of logical expressions using the laws of Boolean algebra is usually carried out with the aim of minimizing, because the simpler the expression, the smaller the complexity of the logic chain, which is the technical implementation of the logical expression.

The laws of Boolean algebra are presented as a set of axioms and consequences. These can be checked quite simply by substituting different values ​​of the variables.

The technical analogue of any logical expression for a Boolean function is a logic diagram... In this case, the variables on which a Boolean function depends are connected to the external inputs of this circuit, the value of a Boolean function is formed at the external output of the circuit, and each logical operation in a logical an expression is implemented by a logical element.

Thus, for each set of input signals at the output of the logic circuit, a signal is generated that corresponds to the value of a boolean function of this set of variables (further on, we will use the following convention: 0 — low signal level, 1 — high level of signal).

When constructing logic circuits, we will assume that the variables are fed to the input in a paraphase code (that is, both direct and inverse values ​​of the variables are available).

Table 1 shows the conventional graphic designations of some logic elements in accordance with GOST 2.743-91, as well as their foreign counterparts.

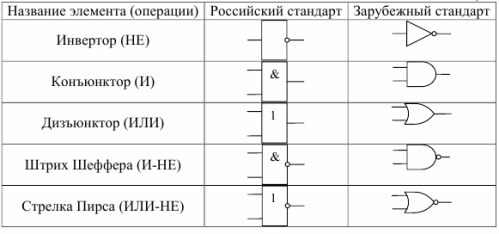
In addition to the elements that perform the three operations of Boolean algebra (AND, OR, NOT), in tab. 1 shows the elements that perform operations derived from the main:

— AND -NOT — negation of logical multiplication, also called Schaefer move (denoted by |)

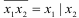
— OR -NOT — negation of logical complement, also called Peirce's arrow (denoted by ?)

By serially connecting logic gates together, you can implement any Boolean function.

Structural formulas expressing relay circuits in general, i.e., containing symbols of reacting eagles, cannot be regarded as functions of two values ​​expressing only closed or open circuit. Therefore, when working with such functions, a number of new dependencies arise that go beyond the limits of Boolean algebra.

In Boolean algebra, there are four pairs of basic laws: two displacements, two combinatorial, two distributive, and two legal inversions. These laws establish the equivalence of different expressions, that is, they consider expressions that can be substituted for each other like the substitution of identities in ordinary algebra. As an equivalence symbol we take the symbol which is the same as the equality symbol in ordinary algebra (=).

The validity of the laws of Boolean algebra for contact circuits will be established by considering circuits corresponding to the left and right sides of equivalent expressions.

Travel laws

To add: x + y = y + x

The schematics corresponding to these expressions are shown in Fig. 1, a.

The left and right circuits are normally open circuits, each of which closes when one of the elements (X or Y) is triggered, that is, these circuits are equivalent. For multiplication: x ·y = y ·NS.

The schematics corresponding to these expressions are shown in Fig. 1b, their equivalence is also obvious.

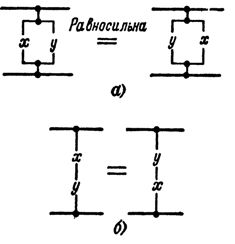
Rice. 1

Laws of Combination

For addition: (x + y) + z = x + (y + z)

For multiplication: (x ·y) ·z = x ·(y ·z)

The pairs of equivalent circuits corresponding to these expressions are shown in Fig. 2, a, b

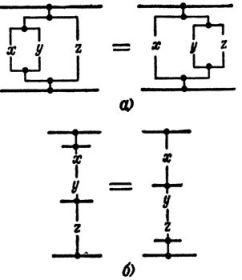
Rice. 2

Distribution Laws

Multiplication versus addition: (x + y) +z = x + (y + z)

Addition vs Multiplication. x ·y + z = (x + z) ·(y + z)

The schematics corresponding to these expressions are shown in Fig. 3, a, b.

Rice. 3.

The equivalence of these schemes can be easily verified by considering different combinations of contact actuation.

Laws of inversion

On addition: NS + c = NS·c

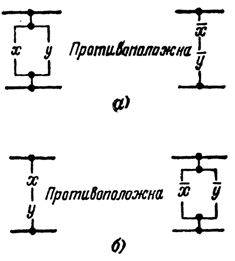
The bar above the left side of the expression is a negation or inversion sign. This sign indicates that the entire function has the opposite meaning with respect to the expression below the negation sign. It is not possible to draw a diagram corresponding to the entire inverse function. But one can draw a diagram corresponding to the expression under the negative sign. Thus, the formula can be illustrated with the diagrams shown in Fig. 4, a.

Rice. 4.

The left diagram corresponds to the expression x + y, and the right one to NS ·c

These two circuits are opposite to each other in operation, namely: if the left circuit with unexcited elements X, Y is an open circuit, then the right circuit is closed. If in the left circuit, when one of the elements is triggered, the circuit closes, and in the right circuit, on the contrary, it opens.

Since, by the definition of negative sign, the function x + y is the inverse of the function x + y, then it is obvious that x + y = NS·in.

Regarding multiplication: NS · c = NS + c

The corresponding schemes are shown in fig. 4, b.

Translocative and combinational and laws and the distributive law of multiplication with respect to addition (correspond to similar laws of ordinary algebra).Therefore, in the case of transformation of structural formulas in the order of addition and multiplication of terms, placement of terms outside brackets and expansion of brackets, you can follow the rules established for working with ordinary algebraic expressions. The distributive law of addition with respect to multiplication and the laws of inversion are specific to Boolean algebra.