Conductors in an electric field

In wires - in metals and electrolytes there are charge carriers. In electrolytes these are ions, in metals - electrons. These electrically charged particles are able to move around the entire volume of the conductor under the influence of an external electrostatic field. The conduction electrons in metals resulting from the condensation of metal vapors due to the sharing of valence electrons are charge carriers in metals.

The strength and potential of the electric field in the conductor

In the absence of an external electric field, a metal conductor is electrically neutral, because inside it the electrostatic field is completely compensated by negative and positive charges in its volume.

If a metal conductor is introduced into an external electrostatic field, then the conduction electrons inside the conductor will begin to redistribute, they will begin to move and move so that everywhere in the volume of the conductor the field of positive ions and the field of conduction electrons will eventually compensate for the external electrostatic field.

Thus, inside a conductor located in an external electrostatic field, at any point the electric field strength E will be zero. The potential difference inside the conductor will also be zero, that is, the potential inside will become constant. That is, we see that the dielectric constant of the metal tends to infinity.

But at the surface of the wire, the intensity E will be directed normal to that surface, because otherwise the voltage component directed tangentially to the surface of the wire would cause charges to move along the wire, which would contradict the real, static distribution. Outside, outside the wire, there is an electric field, which means there is also a vector E perpendicular to the surface.

As a result, in a steady state, a metal conductor placed in an external electric field will have a charge of the opposite sign on its surface, and the process of this establishment takes nanoseconds.

Electrostatic shielding is based on the principle that an external electric field does not penetrate the conductor. The force of the external electric field E is compensated by the normal (perpendicular) electric field on the surface of the conductor En, and the tangential force Et is equal to zero. It turns out that the conductor in this situation is completely equipotential.

At any point on such a conductor φ = const, since dφ / dl = — E = 0. The surface of the conductor is also equipotential, since dφ / dl = — Et = 0. The potential of the surface of the conductor is equal to the potential of its volume. The uncompensated charges on a charged conductor, in such a situation, reside only at its surface, where the charge carriers are repelled by Coulomb forces.

According to the Ostrogradsky-Gauss theorem, the total charge q in the volume of the conductor is zero, since E = 0.

Determination of the strength of the electric field near the conductor

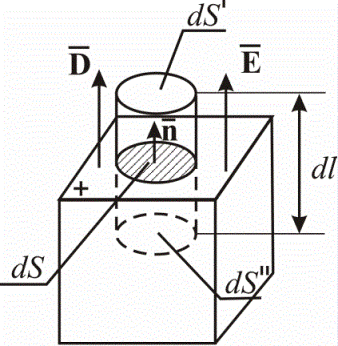
If we choose the area dS of the surface of the wire and build on it a cylinder with generators of height dl perpendicular to the surface, then we will have dS '= dS' '= dS. The electric field strength vector E is perpendicular to the surface and the electric displacement vector D is proportional to E, therefore the flux D through the side surface of the cylinder will be zero.

The flux of the electric displacement vector Фd through dS» is also zero, since dS» is inside the conductor and there E = 0, therefore D = 0. Therefore, dFd through the closed surface is equal to D through dS', dФd = Dn * dS. On the other hand, according to the Ostrogradsky-Gauss theorem: dФd = dq = σdS, where σ is the surface charge density on dS. From the equality of the right sides of the equations it follows that Dn = σ, and then En = Dn / εε0 = σ / εε0.

Conclusion: The strength of the electric field near the surface of a charged conductor is directly proportional to the surface charge density.

Experimental verification of charge distribution on a wire

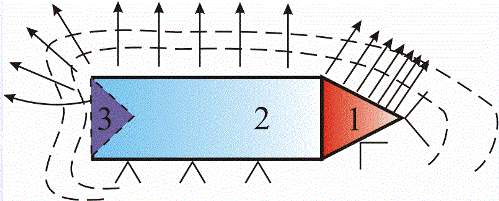
In places with different electric field strength, the paper petals will diverge in different ways. On the surface of a smaller radius of curvature (1) — the maximum, on the side surface (2) — the same, here q = const, that is, the charge is uniformly distributed.

An electrometer, a device for measuring potential and charge on a wire, would show that the charge at the tip is maximum, at the side surface it is less, and the charge on the inner surface (3) is zero.The strength of the electric field at the top of the charged wire is greatest.

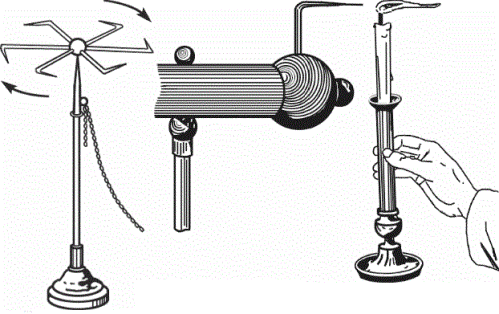
Since the electric field strength E at the tips is high, this leads to charge leakage and ionization of the air, which is why this phenomenon is often undesirable. Ions carry the electrical charge from the wire and the ion wind effect occurs. Visual demonstrations reflecting this effect: blowing out a candle flame and Franklin's wheel. This is a good basis for building an electrostatic motor.

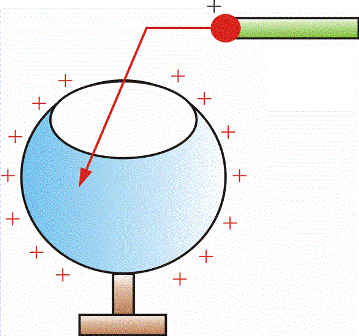
If a metal charged ball touches the surface of another conductor, then the charge will be partially transferred from the ball to the conductor and the potentials of that conductor and the ball will equalize. If the ball is in contact with the inner surface of the hollow wire, then all the charge from the ball will be completely distributed only on the outer surface of the hollow wire.

This will happen whether the potential of the ball is greater than that of the hollow wire or less. Even if the potential of the ball before contact is less than the potential of the hollow wire, the charge from the ball will flow completely, because when the ball moves into the cavity, the experimenter will do work to overcome the repulsive forces, i.e. , the potential of the ball will grow, the potential energy of the charge will increase.

As a result, charge will flow from a higher potential to a lower one. If we now transfer the next part of the charge on the ball to the hollow wire, then even more work will be required. This experiment clearly reflects the fact that potential is an energy characteristic.

Robert Van De Graaf

Robert Van De Graaff (1901 — 1967) was a brilliant American physicist. In 1922Robert graduated from the University of Alabama, later, from 1929 to 1931, worked at Princeton University, and from 1931 to 1960 at the Massachusetts Institute of Technology. He holds a number of research papers on nuclear and accelerator technology, the idea and implementation of the tandem ion accelerator, and the invention of a high voltage electrostatic generator, the Van de Graaf generator.

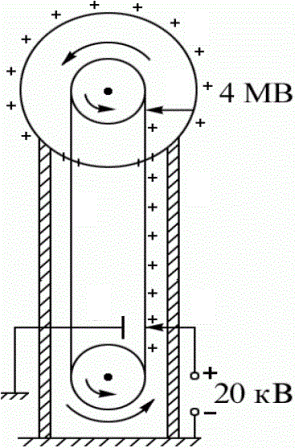
The principle of operation of the Van De Graaff generator is somewhat reminiscent of the experiment with the transfer of charge from a ball to a hollow sphere, as in the experiment described above, but here the process is automated.

The conveyor belt is positively charged using a high voltage DC source, then the charge is transferred with the movement of the belt into the interior of a large metal sphere, where it is transferred from the tip to it and distributed on the outer spherical surface. Thus the potentials with respect to earth are obtained in millions of volts.

Currently, there are van de Graaff accelerator generators, for example, at the Research Institute of Nuclear Physics in Tomsk there is an ESG of this type per million volts, which is installed in a separate tower.

Electrical capacity and capacitors

As mentioned above, when a charge is transferred to a conductor, a certain potential φ will appear on its surface. And for different wires this potential will differ, even if the amount of charge transferred to the wires is the same. Depending on the shape and size of the wire, the potential can be different, but one way or another it will be proportional to the charge and the charge will be proportional to the potential.

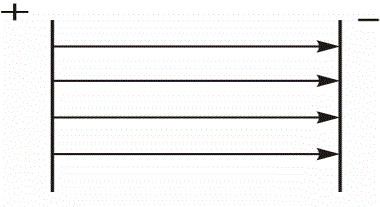
The ratio of the sides is called capacity, capacity or simply capacity (when clearly implied by the context).

Electrical capacitance is a physical quantity that is numerically equal to the charge that must be reported to a conductor to change its potential by one unit. In the SI system, electrical capacity is measured in farads (now «farad», formerly «farad») and 1F = 1C / 1V. So, the surface potential of a spherical conductor (ball) is φsh = q / 4πεε0R, therefore Csh = 4πεε0R.

If we take R equal to the radius of the Earth, then the electric capacitance of the Earth, as a single conductor, will be equal to 700 microfarads. Important! This is the electrical capacitance of the Earth as a single conductor!

If you bring another wire to one wire, then due to the phenomenon of electrostatic induction, the electrical capacity of the wire will increase. So, two conductors located close to each other and representing the plates are called a capacitor.

When the electrostatic field is concentrated between the plates of the capacitor, that is, inside it, external bodies do not affect its electrical capacity.

Capacitors are available in flat, cylindrical and spherical capacitors. Since the electric field is concentrated inside, between the plates of the capacitor, the lines of electric displacement, starting from the positively charged plate of the capacitor, end in its negatively charged plate. Therefore, the charges on the plates are opposite in sign but equal in magnitude. And the capacitance of the capacitor C = q / (φ1-φ2) = q / U.

The formula for the capacitance of a flat capacitor (for example)

Since the voltage of the electric field E between the plates is equal to E = σ / εε0 = q / εε0S and U = Ed, then C = q / U = q / (qd / εε0S) = εε0S / d.

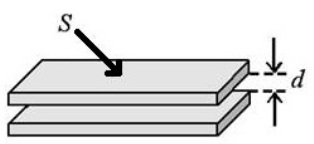
S is the area of ​​the plates; q is the charge on the capacitor; σ is the charge density; ε is the dielectric constant of the dielectric between the plates; ε0 is the dielectric constant of vacuum.

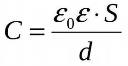
Energy of a charged capacitor

By closing the plates of a charged capacitor together with a wire conductor, one can observe a current that can be of such strength as to melt the wire instantly. Obviously, the capacitor stores energy. What is this energy quantitatively?

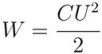
If the capacitor is charged and then discharged, then U' is the instantaneous value of the voltage across its plates. When the charge dq passes between the plates, work will be done dA = U'dq. This work is numerically equal to the loss of potential energy, which means dA = — dWc. And since q = CU, then dA = CU'dU ', and the total work A = ∫ dA. By integrating this expression after previously substituting, we obtain Wc = CU2/2.