Dielectrics in an electric field

All substances known to mankind are capable of conducting electric current to varying degrees: some conduct current better, others worse, others hardly conduct it at all. According to this ability, substances are divided into three main classes:

• Dielectrics;

• Semiconductors;

• Conductors.

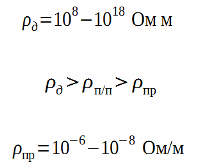
An ideal dielectric contains no charges capable of moving over significant distances, that is, there are no free charges in an ideal dielectric. However, when placed in an external electrostatic field, the dielectric reacts to it. Dielectric polarization occurs, that is, under the action of an electric field, the charges in the dielectric are displaced. This property, the ability of a dielectric to polarize, is the fundamental property of dielectrics.

Thus, the polarization of dielectrics includes three components of polarizability:

• Electronic;

• Jonna;

• Dipole (orientation).

In polarization, the charges are displaced under the action of an electrostatic field. As a result, each atom or each molecule creates an electric moment P.

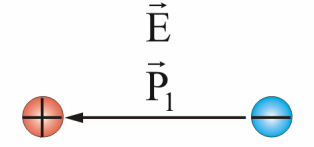
The charges of the dipoles inside the dielectric are mutually compensated, but on the external surfaces adjacent to the electrodes that serve as the source of the electric field, surface-related charges appear that have the opposite sign to the charge of the corresponding electrode.

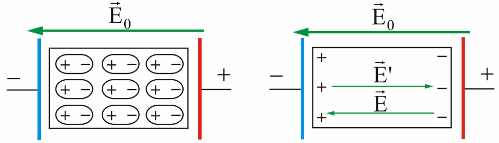
The electrostatic field of the associated charges E' is always directed against the external electrostatic field E0. It turns out that inside the dielectric there is an electric field equal to E = E0 — E '.

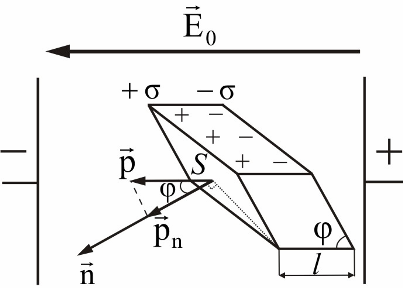
If a body made of a dielectric in the form of a parallelepiped is placed in an electrostatic field of strength E0, then its electric moment can be calculated by the formula: P = qL = σ'SL = σ'SlCosφ, where σ' is the surface density of the associated charges, and φ is the angle between the surface of a face of area S and the normal to it.

In addition, knowing n — the concentration of molecules per unit volume of the dielectric and P1 — the electric moment of one molecule, we can calculate the value of the polarization vector, that is, the electric moment per unit volume of the dielectric.

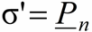
Substituting now the volume of the parallelepiped V = SlCos φ, it is easy to conclude that the surface density of polarization charges is numerically equal to the normal component of the polarization vector at a given point on the surface. The logical consequence is that the electrostatic field E' induced in the dielectric affects only the normal component of the applied external electrostatic field E.

After writing the electric moment of a molecule in terms of voltage, polarizability and dielectric constant of vacuum, the polarization vector can be written as:

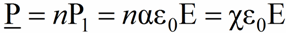
Where α is the polarizability of one molecule of a given substance, and χ = nα is the dielectric susceptibility, a macroscopic quantity characterizing the polarization per unit volume. Dielectric susceptibility is a dimensionless quantity.

Thus, the resulting electrostatic field E changes, compared to E0, only the normal component. The tangential component of the field (directed tangentially to the surface) does not change. As a result, in vector form, the value of the resulting field strength can be written:

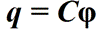
The value of the strength of the resulting electrostatic field in the dielectric is equal to the strength of the external electrostatic field divided by the dielectric constant of the medium ε:

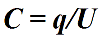
The dielectric constant of the medium ε = 1 + χ is the main characteristic of the dielectric and indicates its electrical properties. The physical meaning of this characteristic is that it shows how many times the field strength E in a given dielectric medium is smaller than the strength E0 in a vacuum:

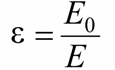
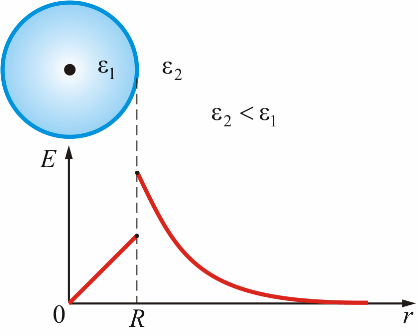
When passing from one medium to another, the strength of the electrostatic field changes sharply, and the graph of the dependence of the field strength on the radius of a dielectric ball in a medium with a dielectric constant ε2 different from the dielectric constant of the ball ε1 reflects this:

Ferroelectrics

1920 was the year of the discovery of the phenomenon of spontaneous polarization. The group of substances susceptible to this phenomenon is called ferroelectrics or ferroelectrics. The phenomenon occurs due to the fact that ferroelectrics are characterized by an anisotropy of properties, in which ferroelectric phenomena can be observed only along one of the crystal axes. In isotropic dielectrics, all molecules are polarized in the same way.For anisotropic — in different directions, the polarization vectors are different in direction.

Ferroelectrics are distinguished by high values ​​of the dielectric constant ε in a certain temperature range:

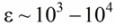
In this case, the value of ε depends on both the external electrostatic field E applied to the sample and the history of the sample. The dielectric constant and electric moment here nonlinearly depend on the force E, therefore ferroelectrics belong to nonlinear dielectrics.

Ferroelectrics are characterized by the Curie point, that is, starting from a certain temperature and higher, the ferroelectric effect disappears. In this case, a phase transition of the second order occurs, for example, for barium titanate, the temperature of the Curie point is + 133 ° C, for Rochelle salt from -18 ° C to + 24 ° C, for lithium niobate + 1210 ° C.

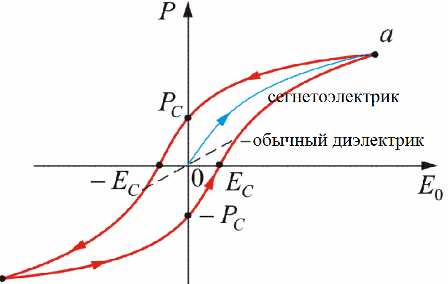
Since dielectrics are nonlinearly polarized, dielectric hysteresis takes place here. Saturation occurs at point «a» of the graph. Ec — coercive force, Pc — residual polarization. The polarization curve is called the hysteresis loop.

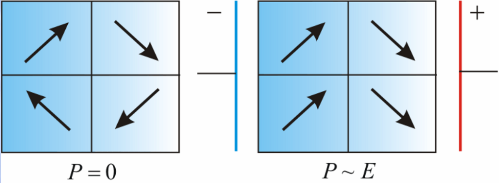
Due to the tendency towards a potential energy minimum, as well as due to defects inherent in their structure, ferroelectrics are internally broken into domains. The domains have different polarization directions and in the absence of an external field their total dipole moment is almost zero.

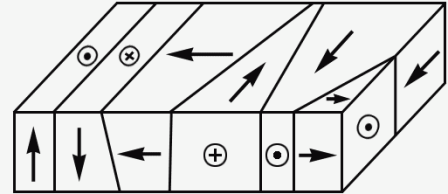
Under the action of the external field E, the boundaries of the domains are shifted, and some of the regions polarized with respect to the field contribute to the polarization of the domains in the direction of the field E.

A vivid example of such a structure is the tetragonal modification of BaTiO3.

In a sufficiently strong field E, the crystal becomes single-domain, and after switching off the external field, the polarization remains (this is the residual polarization Pc).

In order to equalize the volumes of regions with the opposite sign, it is necessary to apply to the sample an external electrostatic field Ec, a coercive field, in the opposite direction.

Electricians

Among the dielectrics, there are electrical analogues of permanent magnets - electrodes. These are such special dielectrics that are able to maintain polarization for a long time even after the external electric field is turned off.

Piezoelectrics

In nature there are dielectrics that are polarized by mechanical impact on them. The crystal is polarized by mechanical deformation. This phenomenon is known as the piezoelectric effect. It was opened in 1880 by the brothers Jacques and Pierre Curie.

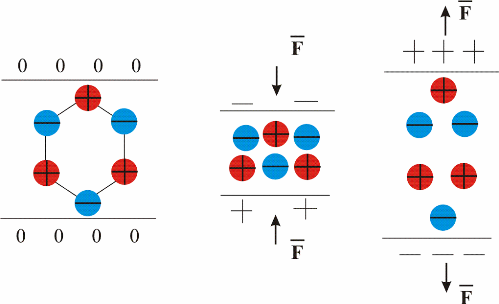
The conclusion is the following. At the metal electrodes located on the surface of the piezoelectric crystal, a potential difference will occur at the moment of deformation of the crystal. If the electrodes are closed by a wire, then an electric current will appear in the circuit.

The reverse piezoelectric effect is also possible — the polarization of the crystal leads to its deformation. When voltage is applied to the electrodes applied to the piezoelectric crystal, a mechanical deformation of the crystal occurs; it will be proportional to the applied field strength E0. Currently, science knows more than 1800 types of piezoelectrics. All ferroelectrics in the polar phase exhibit piezoelectric properties.

Pyroelectrics

Some dielectric crystals polarize when heated or cooled, a phenomenon known as pyroelectricity.For example, one end of a pyroelectric sample becomes negatively charged when heated, while the other is positively charged. And when it cools, the end that was negatively charged when heated will become positively charged when it cools. Obviously, this phenomenon is related to a change in the initial polarization of a substance with a change in its temperature.

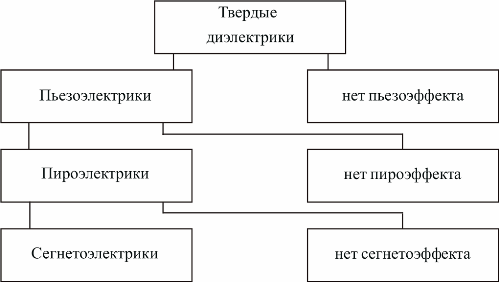
Every pyroelectric has piezoelectric properties, but not every piezoelectric is a pyroelectric. Some of the pyroelectrics have ferroelectric properties, that is, they are capable of spontaneous polarization.

Electric displacement

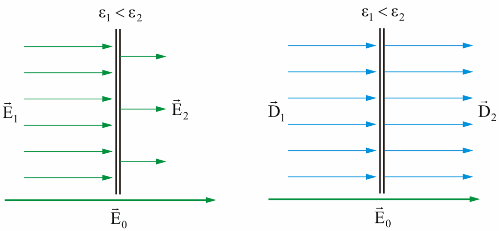
At the boundary of two media with different values ​​of the dielectric constant, the strength of the electrostatic field E changes sharply at the place of sharp changes in ε.

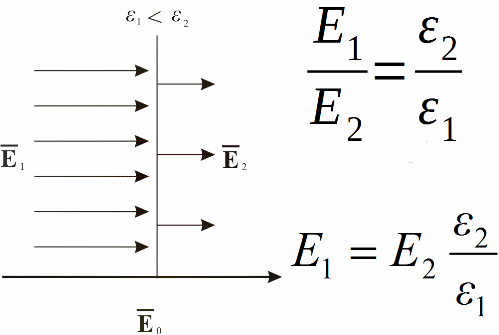
To simplify calculations in electrostatics, the electric displacement vector or electric induction D was introduced.

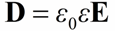
Since E1ε1 = E2ε2, then E1ε1ε0 = E2ε2ε0, which means:

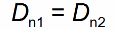
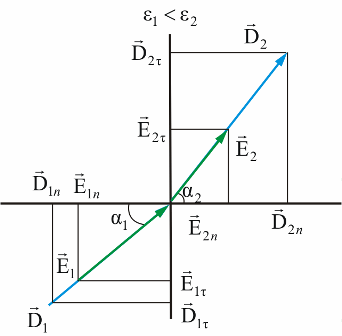
That is, during the transition from one environment to another, the electric displacement vector remains unchanged, that is, the electric induction. This is clearly shown in the figure:

For a point charge in a vacuum, the electric displacement vector is:

Like magnetic flux for magnetic fields, electrostatics uses the flux of an electric displacement vector.

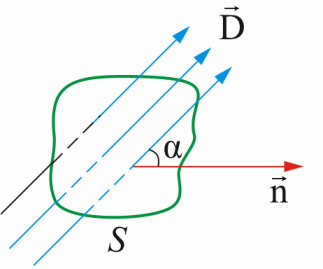
So, for a uniform electrostatic field, when the lines of the electric displacement vector D cross the region S at an angle α to the normal, we can write:

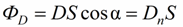
The Ostrogradsky-Gauss theorem for the vector E allows us to obtain the corresponding theorem for the vector D.

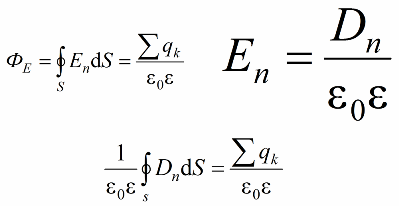
So, the Ostrogradsky-Gauss theorem for the electric displacement vector D sounds like this:

The flux of the vector D through any closed surface is determined only by the free charges, not by all the charges inside the volume bounded by that surface.

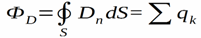
As an example, we can consider a problem with two infinitely extended dielectrics with different ε and with an interface between two media penetrated by an external field E.

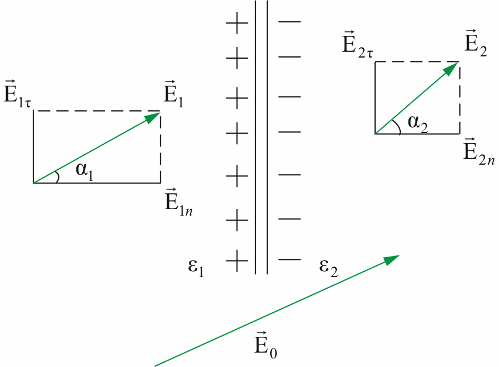
If ε2> ε1, then taking into account that E1n / E2n = ε2 / ε1 and E1t = E2t, since only the normal component of the vector E changes, only the direction of the vector E changes.

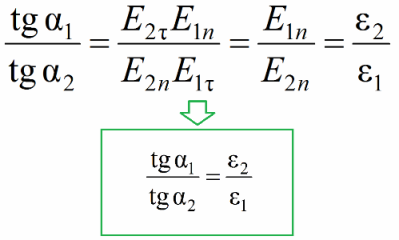
We obtained the law of refraction of the vector intensity E.

The law of refraction for a vector D is similar as D = εε0E and this is illustrated in the figure: