Ampere's Law

In this article, we will talk about Ampere's law, one of the basic laws of electrodynamics. The Ampere's force is at work today in many electrical machines and installations, and thanks to the Ampere's force in the 20th century, advances related to electrification in many areas of production became possible. Ampere's law is steadfast to this day and continues to faithfully serve modern engineering. So let's remember who we owe this progress to and how it all began.

In 1820, the great French physicist Andre Marie Ampere announced his discovery. He spoke at the Academy of Sciences about the phenomenon of the interaction of two current-carrying conductors: conductors with opposite currents repel each other, and with direct currents they attract each other. Ampere also suggested that magnetism was entirely electrical.

For some time, the scientist conducted his experiments and eventually confirmed his assumption. Finally, in 1826, he published The Theory of Electrodynamic Phenomena Derived Exclusively from Experience.From that point on, the idea of ​​a magnetic fluid was dismissed as unnecessary, since magnetism, as it turned out, was caused by electric currents.

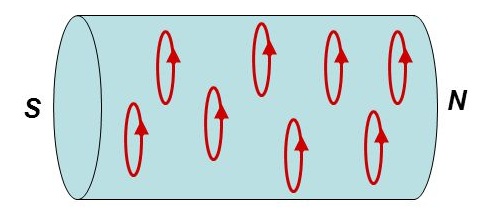
Ampere concluded that permanent magnets also have electric currents inside, circular molecular and atomic currents perpendicular to the axis passing through the poles of a permanent magnet. The coil behaves like a permanent magnet through which current flows in a spiral. Ampere received the full right to confidently assert: "all magnetic phenomena are reduced to electrical actions."

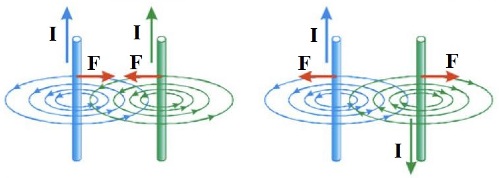
In the course of his research work, Ampere also discovered the relationship between the force of interaction of current elements with the magnitudes of these currents, he also found an expression for this force. Ampère pointed out that the forces of interaction of currents are not central, like gravitational forces. The formula that Ampere derived is included in every textbook on electrodynamics today.

Ampere found that currents from the opposite direction repel and currents from the same direction attract, if the currents are perpendicular then there is no magnetic interaction between them. This is the result of the scientist's investigation of the interactions of electric currents as the true root causes of magnetic interactions. Ampere discovered the law of mechanical interaction of electric currents and thus solved the problem of magnetic interactions.

In order to clarify the laws by which the forces of mechanical interaction of currents are related to other quantities, it is possible to conduct an experiment similar to Ampere's experiment today.To do this, a relatively long wire with current I1 is fixed stationary, and a short wire with current I2 is made movable, for example, the bottom side of the movable frame with current will be the second wire. The frame is connected to a dynamometer to measure the force F acting on the frame when the live conductors are parallel.

Initially, the system is balanced and the distance R between the wires of the experimental setup is significantly smaller compared to the length l of these wires. The purpose of the experiment is to measure the repulsive force of the wires.

The current, in both stationary and moving wires, can be regulated using rheostats. By changing the distance R between the wires, by changing the current in each of them, one can easily find dependencies, see how the strength of the mechanical interaction of the wires depends on the current and on the distance.

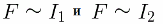
If the current I2 in the moving frame is unchanged and the current I1 in the stationary wire increases by a certain number of times, then the force F of the interaction of the wires will increase by the same amount. Similarly, the situation develops if the current I1 in the fixed wire is unchanged and the current I2 in the frame changes, then the interaction force F changes in the same way as when the current I1 changes in the stationary wire with a constant current I2 in the frame. Thus we reach the obvious conclusion — the force of interaction of the wires F is directly proportional to the current I1 and the current I2.

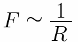
If we now change the distance R between the interacting wires, it turns out that as this distance increases, the force F decreases and decreases by the same factor as the distance R.Thus, the force of the mechanical interaction F of the wires with currents I1 and I2 is inversely proportional to the distance R between them.

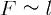
By varying the size l of the movable wire, it is easy to ensure that the force is also directly proportional to the length of the interacting side.

As a result, you can enter the proportionality factor and write:

This formula allows you to find the force F with which the magnetic field generated by an infinitely long conductor with a current I1 acts on a parallel section of a conductor with a current I2, while the length of the section is l and R is the distance between the interacting conductors. This formula is extremely important in the study of magnetism.

The aspect ratio can be expressed in terms of the magnetic constant as:

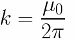
Then the formula will take the form:

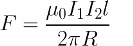
The force F is now called Ampere's force, and the law that determines the magnitude of this force is Ampere's law. Ampere's law is also called a law that determines the force with which a magnetic field acts on a small section of a current-carrying conductor:

«The force dF with which the magnetic field acts on the element dl of the conductor with a current in the magnetic field is directly proportional to the strength of the current dI in the conductor and the vector product of the element with the length dl of the conductor and magnetic induction B «:

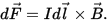
The direction of Ampere's force is determined by the rule for calculating the vector product, which is convenient to remember using the left-hand rule, which refers to basic laws of electrical engineering, and the Ampere force modulus can be calculated by the formula:

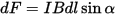
Here, alpha is the angle between the magnetic induction vector and the current direction.

Obviously, the Ampere force is maximum when the element of the current-carrying conductor is perpendicular to the lines of magnetic induction B.

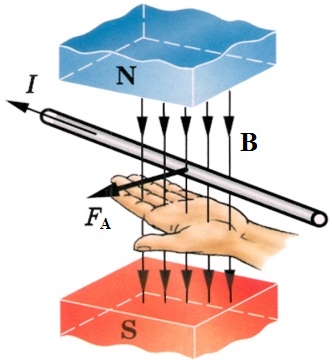
Thanks to Ampere's power, many electrical machines operate today, where current-carrying wires interact with each other and with an electromagnetic field. The majority of generators and motors in one way or another use Ampere power in their work. The rotors of electric motors rotate in the magnetic field of their stators due to Ampere's force.

Electric vehicles: streetcars, electric trains, electric cars — they all use Ampere's power to make their wheels eventually turn. Electric locks, elevator doors, etc. Loudspeakers, loudspeakers - in them the magnetic field of the current coil interacts with the magnetic field of a permanent magnet, forming sound waves. Finally, the plasma is compressed in tokamaks due to Ampere's force.