Basic parameters of alternating current: period, frequency, phase, amplitude, harmonic oscillations

Alternating current is an electric current whose direction and strength change periodically. Since usually the strength of alternating current varies according to a sinusoidal law, alternating current is sinusoidal fluctuations in voltage and current.

Therefore, everything that applies to sinusoidal electrical oscillations is applicable to alternating current. Sinusoidal oscillations are oscillations in which the oscillating value changes according to the sine law. In this article we will talk about AC parameters.

The change in EMF and the change in current of a linear load connected to such a source will follow a sinusoidal law. In this case, alternating EMFs, alternating voltages and currents can be characterized by their main four parameters:

• period;

• frequency;

• amplitude;

• effective value.

There are also additional parameters:

• angular frequency;

• phase;

• immediate value.

Next, we will look at all these parameters separately and together.

Period T.

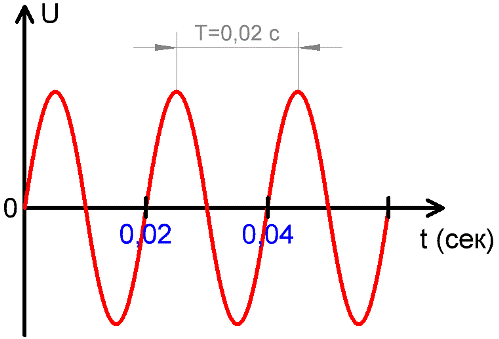
Period — the time it takes for a system that is oscillating to pass through all intermediate states and return to its initial state again.

The period T of an alternating current is the time interval during which the current or voltage makes one complete cycle of changes.

Since the source of alternating current is a generator, the period is related to the speed of rotation of its rotor, and the higher the speed of rotation of the winding or rotor of the generator, the shorter the period of the generated alternating EMF and, accordingly, the alternating current of load, it turns out.

The period is measured in seconds, milliseconds, microseconds, nanoseconds, depending on the particular situation in which this current is considered. The figure above shows how the voltage U changes over time while having a constant characteristic period T.

Frequency f

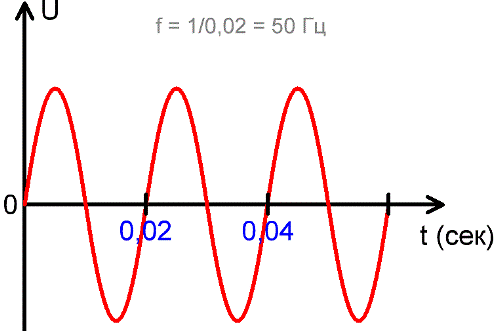
The frequency f is the reciprocal of the period and is numerically equal to the number of periods of current or EMF change in 1 second. That is, f = 1 / T. The unit of measurement of frequency is the hertz (Hz), named after the German physicist Heinrich Hertz, who made a significant contribution to the development of electrodynamics in the 19th century. The shorter the period, the higher the frequency of the EMF or current change.

Today in Russia, the standard frequency of alternating current in electrical networks is 50 Hz, that is, 50 fluctuations of the network voltage appear in 1 second.

In other areas of electrodynamics, higher frequencies are used, for example 20 kHz and more in modern inverters, and up to several MHz in narrower areas of electrodynamics. In the above figure you can see that there are 50 complete oscillations in one second, each lasting 0.02 seconds and 1 / 0.02 = 50.

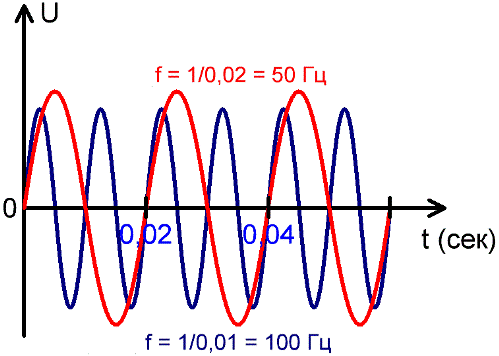
From the graphs of changes in sinusoidal alternating current over time, it can be seen that currents of different frequencies contain a different number of periods in the same time interval.

Angular frequency

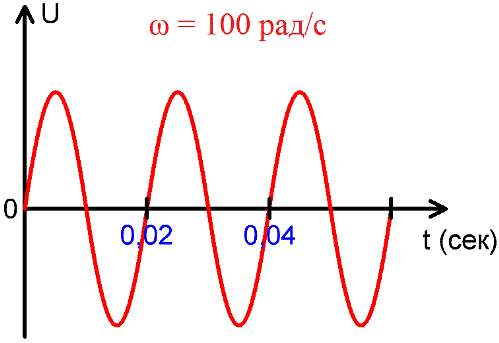
Angular frequency — the number of oscillations made in 2pi sec.

In one period, the phase of the sinusoidal EMF or sinusoidal current changes by 2pi radians or 360 °, therefore the angular frequency of the alternating sinusoidal current is equal to:

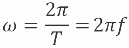
Use the number of oscillations in 2pi sec. (not in 1 sec.) It is convenient because in the formulas expressing the law of the change of voltage and current during harmonic oscillations, expressing the inductive or capacitive resistance of alternating current, and in many other cases the oscillation frequency n appear together with the multiplier 2pi.

Phase

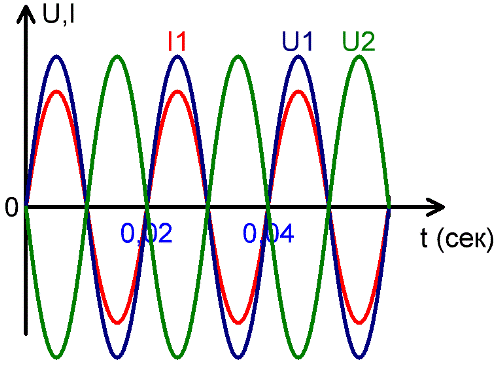
Phase — state, stage of a periodic process. The term phase has a more definite meaning in the case of sinusoidal oscillations. In practice, it is usually not the phase itself that plays a role, but the phase shift between any two periodic processes.

In this case, the term «phase» is understood as a stage of the development of the process, and in this case, in relation to alternating currents and sinusoidal voltages, the phase is called the state of the alternating current at a certain moment in time.

The figures show: the coincidence of voltage U1 and current I1 in phase, voltage U1 and U2 in antiphase, as well as the phase shift between current I1 and voltage U2. Phase shift is measured in radians, parts of a period, in degrees.

See also: What is phase, phase angle and phase shift

Amplitude Um and Im

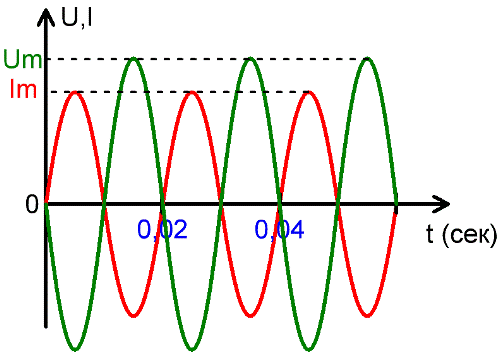
Speaking of the magnitude of sinusoidal alternating current or sinusoidal alternating EMF, the highest value of EMF or current is called amplitude or amplitude (maximum) value.

Amplitude — the largest value of the quantity performing harmonic oscillations (for example, the maximum value of the current strength in alternating current, the deviation of the oscillating pendulum from the equilibrium position), the largest deviation of the oscillating quantity from a certain value, conditionally accepted as initial zero.

Strictly speaking, the term amplitude refers only to sinusoidal oscillations, but it is usually (not quite correctly) applied in the above sense to all oscillations.

If we talk about an alternator, then the EMF of its terminals twice per period reaches an amplitude value, the first of which is + Em, the second is Em, respectively, during the positive and negative half-cycles. The current I behaves similarly and is denoted by Im accordingly.

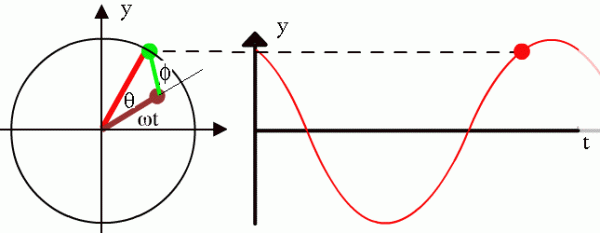
Harmonic vibrations — oscillations in which an oscillating quantity, such as the voltage in an electric circuit, changes with time according to a harmonic sinusoidal or cosine law. Graphically represented by a sinusoidal curve.

Real processes can only approximate harmonic oscillations. However, if the oscillations reflect the most characteristic features of the process, then such a process is considered harmonic, which greatly facilitates the solution of many physical and technical problems.

Movements close to harmonic oscillations occur in various systems: mechanical (oscillations of a pendulum), acoustic (oscillations of an air column in an organ pipe), electromagnetic (oscillations in an LC circuit), etc.The theory of oscillations considers these phenomena, different in physical nature, from a unified point of view and determines their common properties.

It is convenient to represent harmonic oscillations graphically using a vector rotating at constant angular velocity about an axis perpendicular to this vector and passing through its origin. The angular velocity of rotation of the vector corresponds to the circular frequency of the harmonic oscillation.

Vector diagram of a harmonic vibration

A periodic process of any form can be decomposed into an infinite series of simple harmonic oscillations with different frequencies, amplitudes and phases.

Harmonious — a harmonic vibration whose frequency is a whole number of times greater than the frequency of some other vibration, called the fundamental tone. The number of the harmonic indicates how many times its frequency is greater than the frequency of the fundamental tone (for example, the third harmonic is a harmonic vibration with a frequency three times higher than the frequency of the fundamental tone).

Any periodic but not harmonic (that is, different in shape from sinusoidal) oscillations can be represented as a sum of harmonic oscillations—the fundamental tone and a number of harmonics. The more the considered oscillation differs in form from a sinusoidal one, the more harmonics it contains.

Instantaneous value of u and i

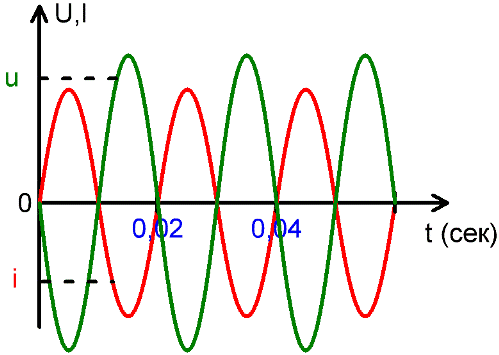
The value of the EMF or current at a certain moment in time is called the instantaneous value, they are denoted by lowercase letters u and i. But since these values ​​change all the time, it is inconvenient to estimate the AC currents and EMFs from them.

RMS values ​​of I, E and U

The ability of alternating current to perform useful work, such as mechanically turning the rotor of a motor or producing heat on a heating device, is conveniently estimated by the effective values ​​of emfs and currents.

So, effective present value is called the value of such a direct current which, when passing through a conductor during one period of the alternating current under consideration, produces the same mechanical work or the same amount of heat as this alternating current.

The RMS values ​​of voltages, emfs and currents are indicated by capital letters I, E and U. For sinusoidal alternating current and for sinusoidal alternating voltage, the effective values ​​are:

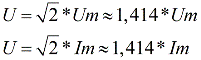
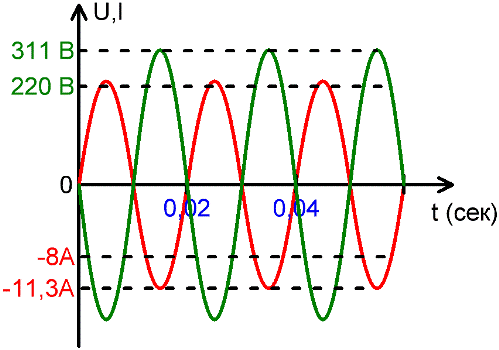
To describe electrical networks, it is convenient to use the effective value of current and voltage. For example, a value of 220-240 volts is the effective value of the voltage in modern household sockets, and the amplitude is much higher — from 311 to 339 volts.

The same with current, for example when they say that a current of 8 amperes flows through a domestic heating device, it means an effective value, while the amplitude is 11.3 amperes.

In one way or another, mechanical work and electrical energy in electrical installations are proportional to the effective values ​​of voltages and currents. A significant part of the measuring devices show exactly the effective values ​​of voltages and currents.