What is internal resistance

Suppose there is a simple electrical closed circuit that includes a current source, for example a generator, galvanic cell or battery, and a resistor of resistance R. Since the current in the circuit is not interrupted anywhere, it also flows inside the source.

In such a situation, we can say that each source has some internal resistance that prevents the current from flowing. This internal resistance characterizes the current source and is denoted by the letter r. For galvanic cell or battery, the internal resistance is the resistance of the electrolyte solution and the electrodes, for a generator - the resistance of the stator windings, etc.

Thus, a current source is characterized by both the magnitude of the EMF and the value of its own internal resistance r — both characteristics indicate the quality of the source.

High-voltage electrostatic generators (such as the Van de Graaf generator or the Wimshurst generator) for example, feature a huge EMF measured in millions of volts, while their internal resistance is measured in the hundreds of megohms, so they are not suitable for obtaining high currents .

On the contrary, galvanic cells (such as a battery) have an EMF of the order of 1 volt, although their internal resistance is of the order of fractions or at most ten ohms, and therefore currents of units and tens of amperes can be obtained from galvanic cells.

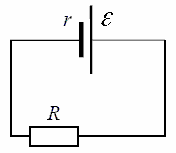
This diagram shows a real source with a connected load. They are defined here EMF source, its internal resistance as well as load resistance. According to Ohm's law for a closed circuit, the current in this circuit will be equal to:

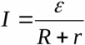
Since the external circuit section is homogeneous, then from Ohm's law the voltage across the load can be found:

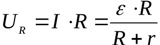
Expressing the resistance of the load from the first equation and substituting its value into the second equation, we obtain the dependence of the voltage in the load on the current in a closed circuit:

In a closed loop, the EMF is equal to the sum of the voltage drop on the external circuit elements and on the internal resistance of the source itself. The dependence of the load voltage on the load current is ideally linear.

The graph shows this, but the experimental data for a real resistor (crosses near the graph) always differ from the ideal:

Experiments and logic show that at zero load current the external circuit voltage is equal to the source emf and at zero load voltage the circuit current is short circuit current… This property of real circuits helps to experimentally find the EMF and internal resistance of real sources.

Experimental detection of internal resistance

To experimentally determine these characteristics, a graph of the dependence of the voltage in the load on the magnitude of the current is built, after which it is extrapolated to the point of intersection with the axes.

At the point of intersection of the graph with the voltage spine is the value of the source emf, and at the point of intersection with the current axis is the value of the short-circuit current. As a result, the internal resistance is found by the formula:

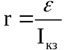
The useful power developed by the source is distributed across the load. The graph of the dependence of this power on the load resistance is shown in the figure. This curve starts from the intersection of the coordinate axes at the zero point, then rises to the maximum power value, then falls to zero with a load resistance equal to infinity.

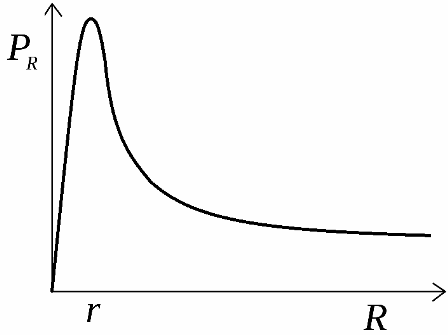
To find the maximum load resistance at which theoretical maximum power will be developed with a given source, the derivative of the power formula with respect to R is taken and set to zero. Maximum power will be developed when the external circuit resistance is equal to the internal source resistance:

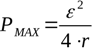
This provision for the maximum power at R = r allows you to experimentally find the internal resistance of the source by plotting the power released at the load versus the value of the load resistance.Finding an actual rather than theoretical load resistance that provides maximum power determines the actual internal resistance of the power supply.

The efficiency of the current source indicates the ratio of the maximum power distributed to the load to the total power that is currently being developed

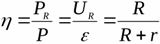
It is clear that if the source develops such power that the maximum possible power for a given source is obtained at the load, then the efficiency of the source will be equal to 50%.