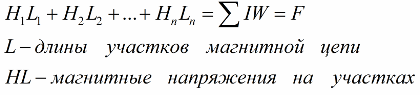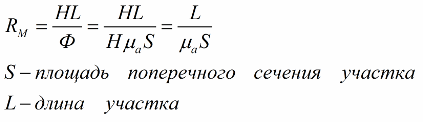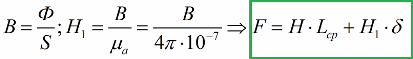What is the magnetic circuit calculation for?

For some technical purposes, here we will consider an example of several of them, it is necessary to calculate the parameters of the magnetic circuits. And the main tool in these calculations is the general operating law. It sounds like this: the line integral of the magnetic field strength vector along a closed loop is equal to the algebraic sum of the currents covered by this loop. The general applicable law is written as follows:

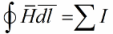
And if in this case the integration circuit covers a coil of W turns through which a current I flows, then the algebraic sum of the currents is the product I * W — this product is called the magnetomotive force of the MDF, which is denoted F. This position is written as follows:

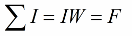
The integration contour is often chosen to coincide with the magnetic field line, in this case the vector product is replaced by the usual product of scalar quantities, the integral is replaced by the sum of the products H * L, then the sections of the magnetic circuit are chosen so , that the force H on them is considered constant. Then the general applicable law takes a simpler form:

Here, by the way, the concept of «magnetic resistance» is introduced, defined as the ratio of the magnetic voltage H * L in a given area to the magnetic flux Ф on it:

For example, consider the magnetic circuit shown in the figure. Here, the ferromagnetic core has the same cross-sectional area S along its entire length. It has a certain length of the center line of the magnetic field L, as well as an air gap with a known sigma value. Through the winding wound of the given magnetic circuit, a certain magnetizing current I flows.

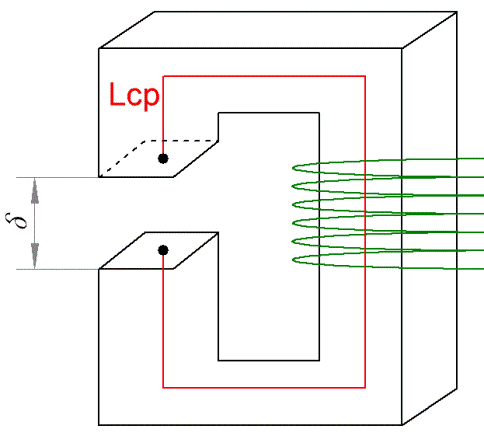
In the direct magnetic circuit calculation problem, based on a given magnetic flux Ф in the magnetic circuit, find the magnitude of the MDF F. First, determine the induction B in the magnetic circuit, for this divide the magnetic flux Ф by the cross-sectional area S of the magnetic circuit .

The second step along the magnetization curve is to find the value of the magnetic field strength H corresponding to the given value of the induction B. Then the total current law is written down, in which all sections of the magnetic circuit are included:

An example of a straightforward problem

Suppose there is a closed magnetic circuit - a toroidal core made of transformer steel, the saturation inductance in it is 1.7 T. It is necessary to find the magnetizing current I at which the core will saturate, if it is known that the winding contains W = 1000 spins. The length of the center line is Lav = 0.5 m. The magnetization curve is given.

Answer:

H * Lav = W * I.

Find H from the magnetization curve: H = 2500A/m.

Therefore, I = H * Lav / W = 2500 * 0.5 / 1000 = 1.25 (amps).

Note.Non-magnetic gap problems are solved in a similar way, then the left side of the equation will have the sum of all HL for the magnetic circuit sections and for the gap section. The strength of the magnetic field in the gap is determined by dividing the magnetic flux (it is the same everywhere along the magnetic circuit) by the area of ​​the gap and by magnetic permeability in the void.

The inverse problem of calculating the magnetic circuit suggests that, based on the known magnetomotive force F, it is necessary to find the magnitude of the magnetic flux.

To solve this problem, they sometimes resort to the magnetic characteristic of the circuit MDF F = f (Ф), where several values ​​​​of the magnetic flux Ф correspond to each of their own values ​​\u200b\u200bof MDS F. So on F, the value of the magnetic flux F.

An example of an inverse problem

A coil of W = 1000 turns is wound on a closed toroidal magnetic circuit (as in the previous direct problem) of transformer steel, a current I = 1.25 amperes flows through the coil. The length of the center line is L = 0.5 m. The cross section of the magnetic circuit is S = 35 sq. Cm. Find the magnetic flux Φ in the core using the reduced magnetization curve.

Answer:

MDS F = I * W = 1.25 * 1000 = 1250 amps. F = HL, which means H = F / L = 1250 / 0.5 = 2500A / m.

From the magnetization curve we find that for a given force the induction is B = 1.7 T.

Magnetic flux Ф = B * S, which means Ф = 1.7 * 0.0035 = 0.00595 Wb.

Note. The magnetic flux throughout the unbranched magnetic circuit will be the same, and even if there is an air gap, then the magnetic flux in it will be the same as the current in an electric circuit. See Ohm's law for a magnetic circuit.

Other examples: Calculation of magnetic circuits