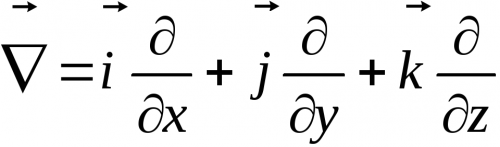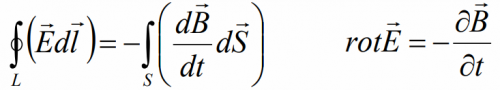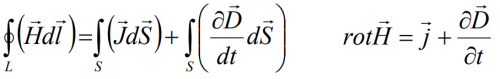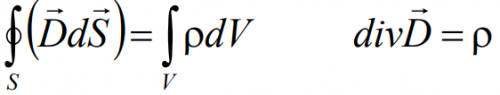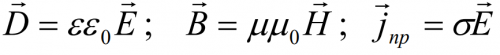Maxwell's equations for an electromagnetic field — the basic laws of electrodynamics

The system of Maxwell's equations owes its name and appearance to James Clerk Maxwell, who formulated and wrote these equations in the late 19th century.

Maxwell James Clark (1831 - 1879) is a famous British physicist and mathematician, a professor at the University of Cambridge in England.

He practically combined in his equations all the experimental results obtained at that time on electricity and magnetism, and gave the laws of electromagnetism a clear mathematical form. The basic laws of electrodynamics (Maxwell's equations) were formulated in 1873.

Maxwell developed Faraday's doctrine of the electromagnetic field into a coherent mathematical theory, from which follows the possibility of wave propagation of electromagnetic processes. It turned out that the speed of propagation of electromagnetic processes is equal to the speed of light (the value of which was already known from experiments).

This coincidence served as the basis for Maxwell to express the idea of ​​the common nature of electromagnetic and light phenomena, i.e. on the electromagnetic nature of light.

The theory of electromagnetic phenomena, created by James Maxwell, found its first confirmation in the experiments of Hertz, who first obtained electromagnetic waves.

As a result, these equations played an important role in the formation of accurate representations of classical electrodynamics. Maxwell's equations can be written in differential or integral form. In practice, they describe in the dry language of mathematics the electromagnetic field and its relation to electric charges and currents in vacuum and in continuous media. To these equations you can add expression for the Lorentz force, in which case we get a complete system of equations of classical electrodynamics.

To understand some of the mathematical symbols used in the differential forms of Maxwell's equations, let us first define such an interesting thing as the nabla operator.

Nabla operator (or Hamilton operator) Is a vector differential operator whose components are partial derivatives with respect to the coordinates. For our real space, which is three-dimensional, a rectangular coordinate system is suitable, for which the operator nabla is defined as follows:

where i, j and k are unit coordinate vectors

The nabla operator, when applied to a field in some mathematical way, gives three possible combinations. These combinations are called:

Gradient — a vector, with its direction indicating the direction of the largest increase of a certain quantity, the value of which varies from one point in space to another (scalar field), and in magnitude (module) is equal to the growth rate of this quantity in this direction.

Divergence (divergence) — a differential operator that maps a vector field to a scalar (that is, as a result of applying the differentiation operation to a vector field, a scalar field is obtained), which determines (for each point) "how much the field enters and leaves a small neighborhood of a given point diverges ”, more precisely how different the inflows and outflows are.

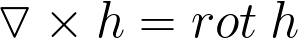
Rotor (vortex, rotation) is a vector differential operator over a vector field.

Now think straight Maxwell's equations in integral (left) and differential (right) formcontaining the fundamental laws of electric and magnetic fields, including electromagnetic induction.

Integral form: the circulation of the electric field strength vector along an arbitrary closed loop is directly proportional to the rate of change of the magnetic flux through the region bounded by this loop.

Differential form: every change in the magnetic field produces an eddy electric field proportional to the rate of change of the magnetic field induction.

Physical meaning: any change in the magnetic field over time causes the appearance of an eddy electric field.

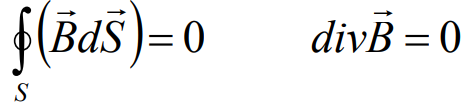
Integral form: the magnetic field induction flux through an arbitrary closed surface is zero. This means that there are no magnetic charges in nature.

Differential form: the flux of field lines of induction of a magnetic field of infinite elementary volume is equal to zero, since the field is eddy.

Physical meaning: in nature there are no sources of magnetic field in the form of magnetic charges.

Integral form: the circulation of the magnetic field strength vector along an arbitrary closed loop is directly proportional to the total current crossing the surface covered by this loop.

Differential Form: An eddy magnetic field exists around any current-carrying conductor and around any alternating electric field.

Physical meaning: the flow of conducting current through wires and the changes in the electric field with time lead to the appearance of an eddy magnetic field.

Integral form: the flux of the electrostatic induction vector through an arbitrary closed surface that encloses the charges is directly proportional to the total charge located inside that surface.

Differential form: the flux of the induction vector of the electrostatic field from an infinite elementary volume is directly proportional to the total charge in that volume.

Physical meaning: the source of the electric field is an electric charge.

The system of these equations can be supplemented with a system of so-called material equations that characterize the properties of the material medium filling the space: