Electromagnetic vibrations — without damping and forced vibrations

Electromagnetic vibrations in a circuit consisting of an inductor and a capacitor occur due to the periodic conversion of electrical energy into magnetic energy and vice versa. In this case, the electric charge on the plates of the capacitor and the magnitude of the current through the coil periodically change.

Electromagnetic vibrations are free and forced. Free oscillations, as a rule, are damped due to non-zero loop resistance, and forced oscillations are usually self-oscillations.

Acquire in a vibrating circuit free oscillations, we first need to bring this system out of equilibrium: inform the capacitor with an initial charge q0 or somehow initiate a current pulse I0 through the coil.

This will serve as a kind of impulse and free electromagnetic oscillations will occur in the circuit - the process of alternating charging and discharging of the capacitor through the inductive coil will begin and, accordingly, the variable rise and fall of the coil's magnetic field

Oscillations that are maintained in a circuit by an external alternating electromotive force are called forced oscillations. So, as you already understood, an example of the simplest oscillating system in which free electromagnetic oscillations can be observed is an oscillating circuit consisting of a capacitor of electric capacity C and a coil of inductance L.

In a real oscillatory circuit, the process of recharging the capacitor is periodically repeated, but the oscillations quickly die out because the energy is dissipated mainly on the active resistance R of the coil wire.

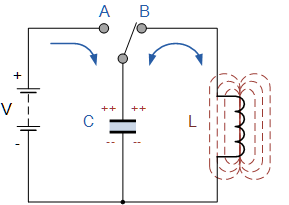
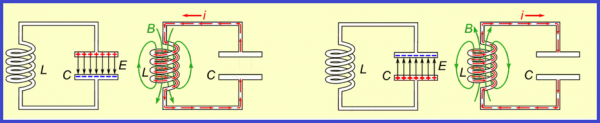
Consider a circuit with an ideal oscillating circuit. Let us first charge the capacitor from the battery — we will give it the initial charge q0, that is, we will fill the capacitor with energy. This will be the maximum energy of the capacitor We.

The next step is to disconnect the capacitor from the battery and connect it in parallel with the inductor. At this point, the capacitor will begin to discharge and an increasing current will appear in the coil circuit. The longer the capacitor discharges, the more charge from it gradually passes into the coil, the greater the current in the coil becomes, thus the coil stores energy in the form of a magnetic field.

This process does not take place instantaneously, but gradually, since the coil has inductance, which means that the phenomenon of self-induction occurs, which consists in the fact that the coil anyway resists the increase in current. At some point, the magnetic field energy of the coil reaches the maximum possible value Wm (depending on how much charge was initially transferred to the capacitor and what the resistance of the circuit is).

Also, due to the phenomenon of self-induction, the current through the coil is maintained in the same direction, but its magnitude decreases and the electric charge eventually accumulates in the capacitor again. In this way, the capacitor is recharged. Its plates now have opposite charge signs than at the beginning of the experiment, when we connected the capacitor to the battery.

The capacitor energy has reached the maximum possible value for this circuit. The current in the circuit has stopped. Now the process begins to go in the opposite direction. And this will continue again and again, that is, there will be free electromagnetic oscillations.

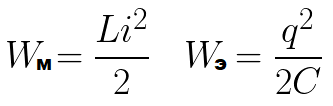
If the active resistance of the circuit R is equal to zero, then the voltage across the capacitor plates and the current through the coil will vary infinitely according to the harmonic law - cosine or sine. This is called harmonic vibration. The charge on the capacitor plates would also change according to a harmonic law.

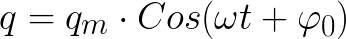
There is no loss in the ideal cycle. And if it were, then the period of free oscillations in the circuit would depend only on the value of the capacitance C of the capacitor and the inductance L of the coil. This period can be found (for an ideal loop with R = 0) using Thomson's formula:

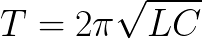
The corresponding frequency and cycle frequency are found for an ideal lossless circuit using the following formulas:

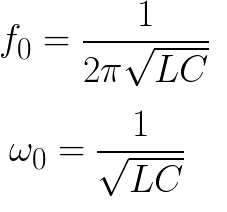
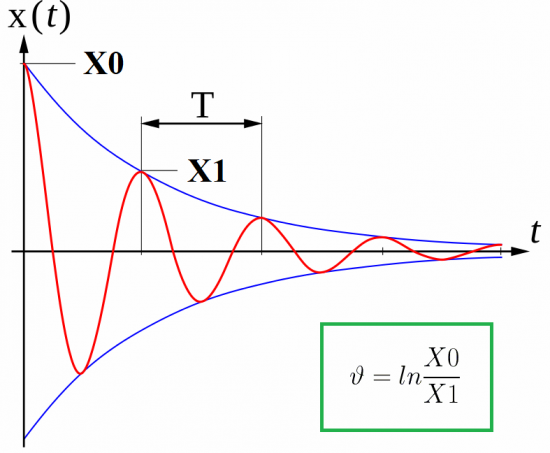
But ideal circuits do not exist and electromagnetic oscillations are damped due to losses due to heating of the wires. Depending on the value of the circuit resistance R, each subsequent maximum capacitor voltage will be lower than the previous one.

In connection with this phenomenon, such a parameter as the logarithmic decrement of oscillations or damping decrement is introduced in physics. It is found as the natural logarithm of the ratio of two consecutive maxima (of the same sign) of the oscillations:

The logarithmic oscillation reduction is related to the ideal oscillation period by the following relationship, where an additional parameter can be introduced, the so-called Damping factor:

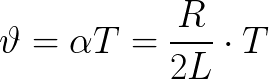
Damping affects the frequency of free vibrations. Therefore, the formula for finding the frequency of free damped oscillations in a real oscillating circuit differs from the formula for an ideal circuit (the damping factor is taken into account):

To make oscillations in the circuit unmuted, it is necessary to replenish and compensate for these losses every half-period. This is achieved in continuous oscillation generators, where the external EMF source compensates the heat losses with its energy. Such a system of oscillations with an external EMF source is called self-oscillating.