Star and triangle connection

If there are three resistances forming three nodes, then such resistances form a passive triangle (Fig. 1, a), and if there is only one node, then a passive star (Fig. 1, b). The word "passive" means that there are no sources of electrical energy in this circuit.

Let's denote the resistances in the delta circuit with capital letters (RAB, RBD, RDA), and in the star circuit with small letters (ra, rb, rd).

Converting a triangle to a star

The passive delta circuit of resistances can be replaced by an equivalent passive star circuit, while all the currents in the branches that have not undergone transformation (that is, everything in Fig. 1, a and 1, b is outside the dotted curve) remain unchanged ...

For example, if currents flow (or leave) to nodes A, B, D in the delta circuit AzA, AzB, and Azd, then in the equivalent star circuit to points A, B, D the same currents will flow (or will flow) AzA, AzB, and Azd.

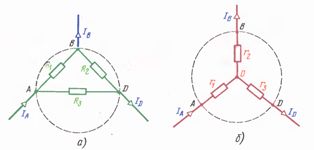
Rice. 1 Star and delta connection diagrams

Calculation of the resistances in the star circuit ra, rb, rd according to the known resistances of the triangle, they are produced by the formulas

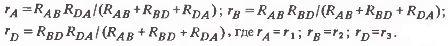
These expressions are formed according to the following rules. The denominators for all expressions are the same and represent the sum of the resistances of the triangle, each numerator being the product of those resistances which in the triangle diagram are in close proximity to the point to which the resistances of the star defined in this expression are adjacent.

For example, the resistance rA in the star scheme is adjacent to point A (see Fig. 1, b). Therefore, in the numerator you need to write the product of the resistances RAB and PDA, since in the triangle diagram these resistances are adjacent to the same point A, etc. If the resistances of the star ra, rb, rd, then you can calculate the resistance of the equivalent triangle RAB, RBD, RDA by the formulas:

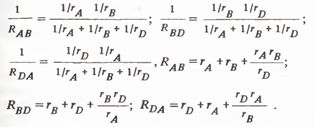
It can be seen from the above formulas that the numerators of all expressions are the same and represent paired combinations of the star resistances, and the denominator contains the resistance adjacent to the star point that is not adjacent to the desired delta resistance.

For example, you need to define R1, that is, the resistance adjacent in the delta circuit to points A and B, therefore the denominator must have resistance re = rd, since this resistance in the star circuit is not adjacent to either point A or point B etc.

Converting a resistance delta with a voltage source to an equivalent star

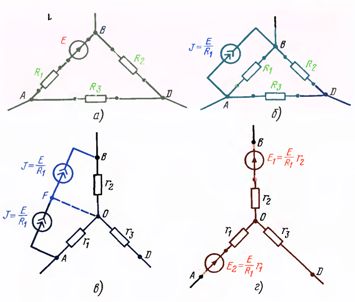
Let there be a chain (Fig. 2, a).

Rice. 2. Converting a resistance triangle with a voltage source into an equivalent star

It is required to transform the given triangle into a star.If there is no source E in the circuit, then the transformation can be done using the formulas for transforming a passive delta into a passive star. However, these formulas are valid only for passive circuits, therefore, in circuits with sources it is necessary to make a number of transformations.

We replace the voltage source E with an equivalent current source, diagram Fig. 2, and has the form of fig. 2, b. As a result of the transformation, a passive triangle R1, R2, R3 is obtained, which can be transformed into an equivalent passive star, and between the points AB the source J = E / Rt remains unchanged.

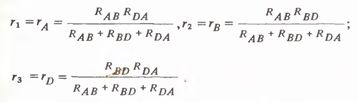
We divide the source J and connect point F to point 0 (shown by a dotted line in Fig. 2, c). Now the current sources can be replaced by equivalent voltage sources, thus obtaining an equivalent star circuit with voltage sources (Fig. 2, d).