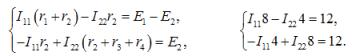Current cycle method
The current loop method is used to calculate resistive linear circuits with constant currents and to calculate complex equivalent circuits of linear circuits with harmonic currents. In this case, loop currents are introduced into the calculation — these are fictitious currents that are closed in independent closed circuits, differing from each other by the presence of at least one new branch.
Circuit calculation method by the current loop method
In the loop current method, the calculated (loop) currents assumed to flow in each of the independent loops are taken as unknown quantities. Thus, the number of unknown currents and equations in the system is equal to the number of independent loops of the circuit.
The calculation of branch currents by the current loop method is carried out in the following order:
1 We draw a schematic diagram of the circuit and label all the elements.
2 Define all independent contours.
3 We arbitrarily set the direction of flow of the loop currents in each of the independent loops (clockwise or counterclockwise). Let us denote these currents.To number the loop currents, you can use Arabic two-digit numbers (I11, I22, I33, etc.) or Roman numerals.
4 From Kirchhoff's second law, in terms of loop currents, we formulate equations for all independent loops. When writing an equation, keep in mind that the direction of the bypass of the loop for which the equation is made coincides with the direction of the loop current of that loop. The fact that two loop currents flow in adjacent branches belonging to two circuits must also be taken into account. The voltage drop of consumers in such branches must be taken from each current separately.
5 We solve the resulting system in terms of loop currents by each method and determine them.
6 We arbitrarily set the direction of the real currents of all branches and label them. Actual currents should be marked in such a way that they are not confused with circuit currents. Single Arabic numerals (I1, I2, I3, etc.) may be used to number the real currents.
7 We pass from loop currents to real ones, assuming that the real branch current is equal to the algebraic sum of the loop currents flowing along this branch.
In algebraic summation, without changing the sign, the loop current is taken, the direction of which coincides with the assumed direction of the real branch current. Otherwise, the loop current is multiplied by minus one.
An example of calculating a complex circuit using the method of loop currents
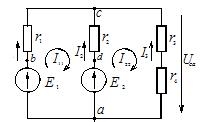
In the circuit shown in Figure 1, calculate all the currents using the current loop method. Circuit parameters: E1 = 24 V, E2 = 12 V, r1 = r2 = 4 Ohm, r3 = 1 Ohm, r4 = 3 Ohm.
Rice. 1. Electrical diagram for an example of calculation by the method of loop currents
Answer.To calculate a complex circuit using this method, it is enough to compose two equations according to the number of independent loops. The loop currents are clockwise and denote I11 and I22 (see Figure 1).
According to Kirchhoff's second law with respect to loop currents, we form the equations:
We solve the system and obtain the loop currents I11 = I22 = 3 A.
We arbitrarily set the direction of the real currents of all branches and label them. In figure 1 these currents are I1, I2, I3. The direction of these currents is the same — vertically upwards.
We pass from loop currents to real ones. Only one loop I11 flows in the first branch. Its direction coincides with the direction of the real branch current. In this case, the actual current I1 + I11 = 3 A.
The real current of the second branch is formed by two loops I11 and I22. Current I22 coincides in direction with the real one, and I11 is directed to the real one. As a result, I2 = I22 — I11 = 3 — 3 = 0A.
Only loop current I22 flows in the third branch. The direction of this current is opposite to the real one, so for I3 it is possible to write I3 = -I22 = -3A.
It should be noted, as a positive fact, that in the method of loop currents compared to the solution for Kiehoff's Laws NS is for solving a system of lower order equations. However, this method does not immediately allow to determine the real currents of the branches.