Calculation of AC circuits

The mathematical expression for sinusoidal current can be written as:
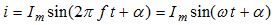
where, I — instantaneous current value indicating the amount of current at a certain moment in time, I am — peak (maximum) value of the current, the expression in brackets is the phase that determines the value of the current at time t, f — the frequency of the alternating current is the reciprocal of the period of change of the sinusoidal value T, ω — angular frequency, ω = 2πf = 2π / T, α — initial phase, shows the value of the phase at time t = 0.
A similar expression can be written for a sinusoidal AC voltage:
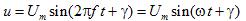
Instantaneous values of current and voltage were agreed to be denoted by lowercase Latin letters i, u, and maximum (amplitude) values - by uppercase Latin letters I, U with an index m.
To measure the magnitude of an alternating current, they most often use an effective (effective) value, which is numerically equal to such a direct current, which during the alternating period releases the same amount of heat into the load as alternating current.
AC rms:
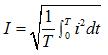
Capital printed Latin letters I, U without subscript are used to indicate effective values of current and voltage.
In sinusoidal current circuits, there is a relationship between the amplitude and the effective values:
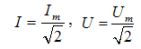
In AC circuits, a change in supply voltage over time results in a change in current as well as in the magnetic and electric field associated with the circuit. The result of these changes is the appearance EMF of self-induction and mutual induction in circuits with inductors and in circuits with capacitors, charging and discharging currents occur, which create a phase shift between voltages and currents in such circuits.
The noted physical processes are taken into account by introducing reactants, in which, unlike active ones, there is no transformation of electrical energy into other types of energy. The presence of current in a reactive element is explained by the periodic exchange of energy between such an element and the network. All this complicates the calculation of alternating current circuits, since it is necessary to determine not only the magnitude of the current, but also its angle of displacement with respect to the voltage.
Everything basic laws DC circuits are also valid for AC circuits, but only for instantaneous values or values in vector (complex) form. Based on these laws, equations can be drawn up that allow the circuit to be calculated.
Usually, the purpose of calculating an alternating current circuit is to determine currents, voltages, phase angles and powers in individual sections... When drawing up equations for calculating such circuits, conditionally positive directions of EMF, voltages and currents are chosen. The resulting equations for steady-state instantaneous values and a sinusoidal input voltage will contain sinusoidal functions of time.
The analytical calculation of trigonometric equations is inconvenient, time-consuming, and therefore not widely used in electrical engineering. It is possible to simplify the analysis of an AC circuit by exploiting the fact that a sinusoidal function can be conventionally represented as a vector, and the vector in turn can be written in complex number form.
Complex number call an expression of the form:
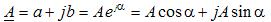
where a is the real (real) part of a complex number, y — imaginary unit, b — imaginary part, A — modulus, α- argument, e — base of natural logarithm.
The first expression is the algebraic notation of a complex number, the second is exponential, and the third is trigonometric. In contrast, in the complex form of designation, the letter denoting an electrical parameter is underlined.
The circuit calculation method based on the use of complex numbers is called the symbolic method... In the symbolic calculation method, all real parameters of the electrical circuit are replaced by symbols in complex notation. After replacing the real parameters of the circuit with their complex symbols, the calculation of AC circuits is carried out according to the methods used for the calculation of DC circuits. The difference is that all mathematical operations must be performed with complex numbers.
As a result of calculating the electrical circuit, the required currents and voltages are obtained in the form of complex numbers. The real rms values of the current or voltage are equal to the modulus of the corresponding complex, and the argument of the complex number indicates the angle of rotation of the vector on the complex plane relative to the positive direction of the real axis. A positive argument rotates the vector counterclockwise, and a negative argument rotates it clockwise.
The calculation of the alternating current circuit ends, as a rule, by composition balance of active and reactive power, which allows you to check the correctness of the calculations.
