Electric field characteristics

The article describes the main characteristics of the electric field: potential, voltage and intensity.

What is an electric field

To create an electric field, it is necessary to create an electric charge. The properties of the space around the charges (charged bodies) differ from the properties of the space in which there are no charges. At the same time, the properties of space, when an electric charge is introduced into it, do not change instantly: the change starts from the charge and spreads with a certain speed from one point in space to another.

In a space containing a charge, mechanical forces acting on other charges introduced into that space are manifested. These forces are not the result of the direct action of one charge on another, but of the action through a qualitatively changed medium.

The space around electric charges, in which the forces that act on the electric charges introduced into it are manifested, is called an electric field.

A charge in an electric field moves in the direction of the force acting on it from the side of the field.The state of rest of such a charge is possible only when some external (external) force is applied to the charge that balances the strength of the electric field.

As soon as the balance between the external force and the field strength is disturbed, the charge starts moving again. The direction of its movement always coincides with the direction of the greater force.

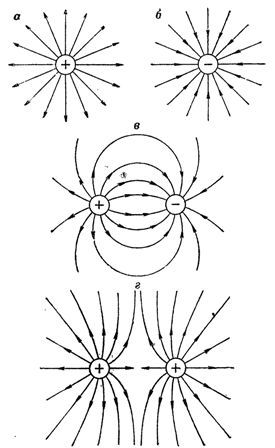
For clarity, the electric field is usually represented by so-called electric field lines. These lines coincide with the direction of the forces acting in the electric field. At the same time, it was agreed to draw so many lines that their number for every 1 cm2 of the area installed perpendicular to the lines was proportional to the strength of the field at the corresponding point.

The direction of the field is usually taken to be the direction of the field strength acting on a positive charge placed in a given field. Positive charges are repelled by positive charges and attracted to negative charges. Therefore, the field is directed from positive to negative charges.

The direction of the lines of force is indicated in the drawings by arrows. Science has proven that the lines of force of an electric field have a beginning and an end, that is, they are not closed by themselves. Based on the assumed direction of the field, we find that the lines of force start with positive charges (positively charged bodies) and end with negative ones.

Rice. 1. Examples of an image of an electric field using lines of force: a — an electric field with a single positive charge, b — an electric field with a single negative charge, c — an electric field of two opposite charges, d — an electric field of two like charges

In fig.1 shows examples of an electric field depicted using lines of force. It must be remembered that electric field lines are only a way of graphically representing a field. There is no greater substance to the line of force concept here.

Coulomb's law

The strength of the interaction between two charges depends on the size and mutual arrangement of the charges, as well as on the physical properties of their environment.

For two electrified physical bodies, the dimensions of which are insignificant compared to the distance between the bodies, the healing of the interaction is determined mathematically as follows:

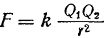
where F is the force of interaction of charges in newtons (N), k — distance between charges in meters (m), Q1 and Q2 — magnitude of electric charges in coulombs (k), k is the proportionality coefficient, the value of which depends on the properties of the medium surrounding the charges.

The above formula reads like this: the force of interaction between two point charges is directly proportional to the product of the magnitudes of these charges and inversely proportional to the square of the distance between them (Coulomb's law).

To determine the proportionality factor k, use the expression k = 1 /(4πεεО).

Electric field potential

An electric field always imparts motion to a charge if the field forces acting on the charge are not balanced by any external forces. This implies that the electric field has potential energy, that is, the ability to do work.

By moving a charge from one point in space to another, the electric field does work, as a result of which the supply of potential energy to the field decreases.If a charge moves in an electric field under the action of some external force acting opposite to the field forces, then work is done not by the electric field forces, but by external forces. In this case, the potential energy of the field not only does not decrease, but, on the contrary, increases.

The work done by an external force moving a charge in an electric field is proportional to the magnitude of the field forces opposing that motion. The work done in this case by external forces is entirely spent on increasing the potential energy of the field. To characterize the field from the side of its potential energy, a quantity called electric field potential is called.

The essence of this quantity is as follows. Suppose the positive charge is outside the electric field under consideration. This means that the field has practically no effect on the given charge. Let an external force introduce this charge into the electric field and, overcoming the resistance to motion exerted by the field forces, move the charge to a given point in the field. The work done by the force, and hence the amount by which the potential energy of the field has increased, depends entirely on the properties of the field. Therefore, this work can characterize the energy of a given electric field.

The electric field energy related to a unit of positive charge placed at a given point in the field is called the field potential at a given point.

If the potential is denoted by the letter φ, the charge by the letter q and the work spent on moving the charge by W, then the field potential at a given point will be expressed by the formula φ = W / q.

It follows that the electric field potential at a given point is numerically equal to the work done by an external force when a unit positive charge moves out of the field toward a given point. Field potential is measured in volts (V). If during the transfer of one coulomb of electricity outside the field to a given point, external forces have done work equal to one joule, then the potential at a given point in the field is equal to one volt: 1 volt = 1 joule / 1 coulomb

Electric field strength

In any electric field, positive charges move from points of higher potential to points of lower potential. On the contrary, negative charges move from points of lower potential to points of higher potential. In both cases, work is done at the expense of potential energy of the electric field.

If we know this work, that is, the amount by which the potential energy of the field has decreased when the positive charge q moves from point 1 of the field to point 2, then it is easy to find the voltage between these points of the field U1,2:

U1,2 = A / q,

where A is the work done by the field forces when the charge q is transferred from point 1 to point 2. The voltage between two points in the electric field is numerically equal to the work done by zero to transfer a unit positive charge from one point in the field to another.

As can be seen, the voltage between two points of the field and the potential difference between the same points represent the same physical unit… Therefore, the terms voltage and potential difference are the same. Voltage is measured in volts (V).

The voltage between two points is equal to one volt if, when transferring one coulomb of electricity from one point of the field to another, the field forces do work equal to one joule: 1 volt = 1 joule / 1 coulomb

Electric field strength

It follows from Coulomb's law that the electric field strength of a given charge acting on another charge placed in this field is not the same at all points of the field. The electric field at any point can be characterized by the magnitude of the force with which it acts on a unit positive charge placed at a given point.

Knowing this value, the force F acting on each charge Q can be determined. You can write that F = Q x E, where F is the force acting on the charge Q placed at a point in the field by the electric field, E is the force acting on a unit positive charge placed at the same point in the field. The quantity E numerically equal to the force experienced by a unit positive charge at a given point in the field is called the electric field strength.