Continuous oscillations and parametric resonance

Continuous vibrations — vibrations whose energy does not change over time. In real physical systems, there are always causes that cause the transition of vibrational energy to thermal energy (e.g. friction in mechanical systems, active resistance in electrical systems).

Therefore, undamped oscillations can only be obtained provided that these energy losses are replenished. Such replenishment occurs automatically in self-oscillating systems due to energy from an external source. Continuous electromagnetic oscillations are extremely widely used. Different generators are used to obtain them.

To make electrical or mechanical vibrations (of an oscillating circle or pendulum) undamped, it is necessary to compensate for resistance or frictional losses at all times.

For example, you can act on the oscillating circuit with an alternating EMF, which will periodically increase the current in the coil and, accordingly, maintain the voltage amplitude in the capacitor.Or you can push the pendulum in a similar way, keeping it swinging harmoniously.

As you know, the magnitude of the energy of the magnetic field of the coil of the oscillating circuit is related to its inductance and current by the following relationship (the second formula isenergy of the electric field of the capacitor same contour contour)

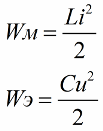
It is clear from the first formula that if we periodically increase the current in the coil, acting on the alternating EMF circuit, then (by increasing or decreasing the second factor in the formula — current) we will periodically replenish this circuit with energy.

Acting on the circuit strictly in time with its natural free oscillations, that is, at the resonant frequency, we will get the phenomenon of electrical resonance, because it is at the resonant frequency oscillating system most intensively absorbs the energy supplied to it.

But what if you periodically change not the second factor (not current or voltage), but the first factor - inductance or capacitance? In this case, the circuit will also undergo a change in its energy.

For example, periodically pushing the core in and out of the coil or pushing in and out of the capacitordielectric, — we also get a very definite periodic change in the energy in the circuit.

We write this position for a unit change in coil inductance:

The most pronounced effect of the swing of the circuit will be if the inductance changes are made just in time. For example, if we take the same circuit at any moment in time, when some current i is already flowing through it, and introduce a core into the coil, then the energy will change by the following amount:

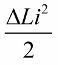
Now let free oscillations appear in the circuit itself, but at the moment when, after a quarter period, the energy has completely passed into the capacitor and the current in the coil has become zero, we will abruptly remove the core from the coil The inductance will return to its original state, to the initial value L. No work needs to be expended against the magnetic field when the core is removed. Therefore, when the core was pushed into the coil, the circuit received energy, since we worked, the value of which:

After a quarter of the period, the capacitor begins to discharge, its energy is again converted into the energy of the magnetic field of the coil. When the magnetic field reaches amplitude, we will press the core sharply again. Again the inductance increased, increased by the same amount.

And again, at zero current, we return the inductance to its original value. As a result, if the energy gains for each half-cycle exceed the resistance losses, the energy of the loop will increase all the time and the oscillation amplitude will increase. This situation is expressed by the inequality:

Here we divided both sides of this inequality by L and wrote down the condition for the possibility of parametric excitation by jumps for a certain value of the logarithmic decrement.

It is recommended to change the inductance (or capacitance) twice per period, therefore the frequency of the parameter change (parametric resonance frequency) should be twice the natural frequency of the oscillating system:

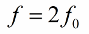
So the path of excitation of oscillations in the circuit has appeared without the need to directly change the EMF or current.The initial fluctuating current in the circuit is always present in one way or another, and that doesn't even take into account interference from radio frequency oscillations in the atmosphere.

If the inductance (or capacitance) does not change in jumps, but harmonically, then the condition for the occurrence of oscillations will look a little different:

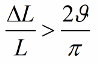
Since capacitance and inductance are circuit parameters (such as the mass of a pendulum or the elasticity of a spring), the method of exciting oscillations is also called parametric excitation.

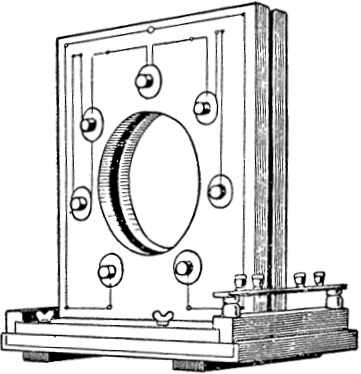
This phenomenon was discovered and practically studied at the beginning of the 20th century by the Soviet physicists Mandelstam and Papalexi. Based on this physical phenomenon, they built the first parametric AC generator with a power of 4 kW and variable inductance.

In the design of the generator, seven pairs of flat coils were located on both sides of the frame, in the cavity of which a ferromagnetic disc with protrusions rotated. When the disk is driven to rotate by a motor, its protrusions periodically move in and out of the space between each pair of coils, thereby changing the inductance and exciting oscillations.