Calculation of capacitor capacitance

Capacitance C is the capacity of the capacitor to accept (store and hold) the quantity of electricity Q in ampere-seconds or the charge Q in pendants. If you tell a body, for example a ball, an electric charge (quantity of electricity) Q, then an electroscope connected between this body and the ground will show a voltage U (Fig. 1). This voltage is proportional to the charge and also depends on the shape and size of the body.

The relationship between charge Q and voltage U is expressed by the formula Q = C ∙ U.

The constant of proportionality C is called the capacitance of the body. If the body has the shape of a ball, the capacitance of the body is proportional to the radius of the ball r.

Rice. 1.

The unit of measurement for capacitance is the farad (F).

The body has a capacitance of 1 F when a charge of 1 k produces a voltage of 1 V. between it and the ground. Farads are a very large unit of measurement, so smaller units are used in practice: microfarad (μF), nanofarad (nF) and picofarad (pF)...

These units are related by the following ratios: 1 Ф = 10 ^ 6 μF; 1 μF = 10 ^ 6 pF; 1 nF = 10 ^ 3 pF.

The capacitance of a ball with a radius of 1 cm is 1.1 pF.

Not only an isolated body can accumulate charge, but also a special device called a capacitor. A capacitor consists of two or more plates (plates) that are separated by a dielectric (insulation).

In fig. 2 shows a circuit with a DC source connected to a capacitor. When switched on, a positive charge +Q is formed in the right plate of the capacitor and a negative charge –Q in the left plate. During capacitor charge a current flows through the circuit, which stops after the end of charging; then the voltage across the capacitor will be equal to e. etc. c. source U. The charge on the capacitor plate, voltage and capacitance are related by the ratio Q = C ∙ U. In this case, an electrostatic field is formed in the dielectric of the capacitor.

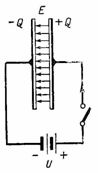
Rice. 2.

The capacity of a capacitor with an air dielectric can be calculated by the formula C = S / (4 ∙ π ∙ d) ∙ 1.11, pF, where S is the area of ​​one plate, cm2; d is the distance between the plates, cm; C is the capacitance of the capacitor, pF.

The capacity of a capacitor consisting of n plates (Fig. 3) is equal to: C = (n-1) ∙ S / (4 ∙ π ∙ d) ∙ 1.11, pF.

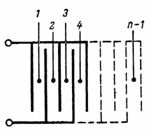
Rice. 3.

If the space between the plates is filled with another dielectric, for example paper, the capacitance of the capacitor will increase by a factor of ε. When paper insulation is used, the capacity will increase 3 times, with mica insulation — 5-8 times, with glass — 7 times, etc. The value of ε is called the dielectric constant of the dielectric.

The general formula for determining the capacitance of a capacitor with dielectric constant ε (epsilon) is: C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, pF.

This formula is useful for calculating small variable capacitors for radios.The same formula can be represented as: C = (ε_0 ∙ ε ∙ S) / d, where ε_0 is the dielectric constant or the dielectric constant of the vacuum (ε_0 = 8.859 ∙ 10 ^ (- 12) F / m); ε is the dielectric constant of the dielectric.

In this formula, the dimensions are replaced in meters, and the capacitance is obtained in farads.

Examples of

1. What is the capacity of the planet Earth, whose radius is r = 6378 km?

Since the capacitance of a sphere with a radius of 1 cm is equal to 1.11 pF, the capacitance of the Earth is: C = 637.8 ∙ 10 ^ 6 ∙ 1.11 = 707.95 ∙ 10 ^ 6 pF = 708 μF. (The capacity of a ball the size of our planet is relatively small. Small-sized electrolytic capacitors have this capacity).

2. Determine the capacitance of a capacitor consisting of two plates, each of which has an area S = 120 cm2.

The plates are separated by a layer of air with a thickness of d = 0.5 cm, C = S / (4 ∙ π ∙ d) ∙ 1.11 = (120 ∙ 1.11) / (4 ∙ π ∙ 0.5) = 21 ,20 pF .. .

3. Determine the capacitance of the capacitor with the data given in the previous example, if the space between the plates is filled with wax paper with a dielectric constant ε = 4, glass (ε = 7), electrical cardboard (ε = 2), mica (ε = 8 ).

A wax paper capacitor has a capacitance C = ε ∙ (S ∙ 1.11) / (4 ∙ π ∙ d) = 4 ∙ 21.2 = 84.8 pF.

The capacitance of a glass capacitor is C = 7 ∙ 21.2 = 148.4 pF.

The capacitance of the cardboard capacitor is C = 2 ∙ 21.2 = 42.3 pF.

The capacitance of the mica capacitor is C = 8 ∙ 21.2 = 169.6 pF.

4. What is the capacitance of an air rotary capacitor for a radio receiver consisting of 20 plates with an area of ​​20 cm2 if the distance between the plates is 0.06 cm (Fig. 149)?

C = (n-1) ∙ (S ∙ 1.11) / (4 ∙ π ∙ d) = (20-1) ∙ (20 ∙ 1.11) / (4 ∙ π ∙ 0.06) = 559, 44 pF.

The capacitor shown in Fig.3, consists of separate simplest capacitors with two plates, the number of which is equal to n-1.

5. A paper capacitor of capacitance C = 2 μF consists of two strips of tinfoil C and two strips of a dielectric made of wax paper B with a dielectric constant ε = 6. The thickness of the wax paper is d = 0.1 mm. The folded strips are rolled up, the leads are made from the steel plates. Determine the length of the condenser steel strip if its width is 4 cm (Fig. 4).

Rice. 4.

First, we determine the area of ​​one strip by the formula C = ε ∙ S / (4 ∙ π ∙ d) ∙ 1.11, whence S = (C ∙ 4 ∙ π ∙ d) / (ε ∙ 1.11) = (2 ∙ 4 ∙ π ∙ 0.01 ∙ 10 ^ 6) / (6 ∙ 1.11); S = 2,000,000 / (6 ∙ 1.11) ∙ 4 ∙ π ∙ 0.01 = 37680 cm2.

The length of each strip is l = 37680/4 = 9420 cm = 94.2 m.