Traction force of electromagnets

The force with which an electromagnet attracts ferromagnetic materials depends on the magnetic flux F or, equivalently, on the induction B and the cross-sectional area of ​​the electromagnet S.

The pressure force of the electromagnet is determined by the formula

F = 40550 ∙ B ^ 2 ∙ S,

where F is the pressure force of the electromagnet, kg (the force is also measured in newtons, 1 kg = 9.81 N or 1 N = 0.102 kg); B — induction, T; S is the cross-sectional area of ​​the electromagnet, m2.

Examples of

1. The faucet electromagnet is a magnetic circuit (Fig. 1). What is the lifting force of a horseshoe crane electromagnet, if the magnetic induction is B = 1 T, and the cross-sectional area of ​​each pole of the electromagnet is S = 0.02 m2 (Fig. 1, b)? Neglect the effect of the gap between the electromagnet and the armature.

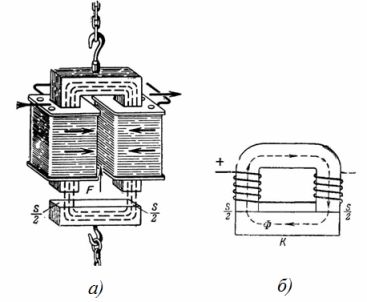
Rice. 1. Lifting electromagnet

F = 40550 ∙ B ^ 2 ∙ S; F = 40550 ∙ 1 ^ 2 ∙ 2 ∙ 0.02 = 1622 kg.

2. A circular steel electromagnet has the dimensions shown in fig. 2, a and b. The lifting force of the electromagnet is 3 T. Determine the cross-sectional area of ​​the electromagnet core, n. p. and the number of turns of the coil at a magnetizing current I = 0.5 A.

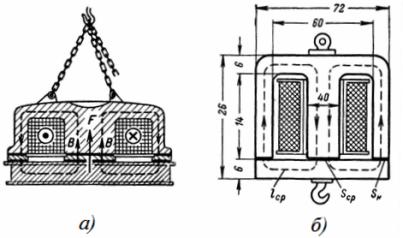
Rice. 2. Round electromagnet

The magnetic flux passes through the circular inner core and returns through the cylindrical body. The cross-sectional areas of the core Sc and the casing Sk are approximately the same, therefore the induction values ​​in the core and the casing are practically the same:

Sc = (π ∙ 40 ^ 2) / 4 = (3.14 ∙ 1600) / 4 = 1256 cm2 = 0.1256 m2,

Sk = ((72 ^ 2-60 ^ 2) ∙ π) / 4 = 3.14 / 4 ∙ (5184-3600) = 1243.5 cm2 = 0.12435 m2;

S = Sc + Sk = 0.24995 m2 ≈0.25 m2.

The required induction in the electromagnet is determined by the formula F = 40550 ∙ B ^ 2 ∙ S,

where B = √ (F / (40550 ∙ S)) = √ (3000 / (40550 ∙ 0.25)) = 0.5475 T.

The voltage at this induction is found on the magnetization curve of the cast steel:

H = 180 A / m.

The average length of the field line (Fig. 2, b) lav = 2 ∙ (20 + 23) = 86 cm = 0.86 m.

Magnetizing force I ∙ ω = H ∙ lav = 180 ∙ 0.86 = 154.8 Av; I = (I ∙ ω) / I = 154.8 / 0.5 = 310 A.

Actually n. s, that is, the current and the number of turns, must be many times greater, since there is an inevitable air gap between the electromagnet and the armature, which significantly increases the magnetic resistance of the magnetic circuit. Therefore, the air gap must be taken into account when calculating the electromagnets.

3. The coil of the electromagnet for the faucet has 1350 turns, a current I = 12 A flows through it. The dimensions of the electromagnet are shown in fig. 3. What weight does the electromagnet lift at a distance of 1 cm from the armature and what weight can it hold after gravity?

Rice. 3. Electromagnetic coil

Most of N. with I ∙ ω is spent on conducting magnetic flux through the air gap: I ∙ ω≈Hδ ∙ 2 ∙ δ.

Magnetizing force I ∙ ω = 12 ∙ 1350 = 16200 A.

Since H ∙ δ = 8 ∙ 10 ^ 5 ∙ B, then Hδ ∙ 2 ∙ δ = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02.

Therefore, 16200 = 8 ∙ 10 ^ 5 ∙ B ∙ 0.02, i.e. B = 1.012T.

We assume that the induction is B = 1 T, since part of n. c. I ∙ ω is spent on conducting magnetic flux in steel.

Let's check this calculation by the formula I ∙ ω = Hδ ∙ 2 ∙ δ + Hс ∙ lс.

The average length of the magnetic line is: lav = 2 ∙ (7 + 15) = 44 cm = 0.44 m.

The intensity Hc at B = 1 T (10000 Gs) is determined from the magnetization curve:

Hc = 260 A / m. I ∙ ω = 0.8 ∙ B ∙ 2 + 2.6 ∙ 44 = 1.6 ∙ 10000 + 114.4 = 16114 Av.

The magnetizing force I ∙ ω = 16114 Av creating an induction B = 1 T is practically equal to the given n. v. I ∙ ω = 16200 Av.

The total cross-sectional area of ​​the core and cone is: S = 6 ∙ 5 + 2 ∙ 5 ∙ 3 = 0.006 m2.

The electromagnet will attract a charge of weight F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 1 ^ 2 ∙ 0.006 = 243.3 kg from a distance of 1 cm.

Since the air gap practically disappears after the armature is attracted, the electromagnet can withstand a much larger load. In this case, the entire n. c. I ∙ ω is spent on conducting magnetic flux only in steel, therefore I ∙ ω = Hс ∙ lс; 16200 = Hs ∙ 44; Hc = 16200/44 = 368 A/cm = 36800 A/m.

At such a voltage, the steel is practically saturated and the induction in it is approximately 2 T. The electromagnet attracts the armature with a force F = 40550 ∙ B ^ 2 ∙ S = 40550 ∙ 4 ∙ 0.006 = 973 kg.

4. The signal (blinker) relay consists of an armored electromagnet 1 with a round core and a valve-type armature 2, which, after supplying current to the electromagnet, attracts and releases the blinker 3, which opens the signal digit (Fig. 4).

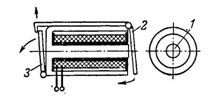
Rice. 4. Armor electromagnet

The magnetizing strength is I ∙ ω = 120 Av, the air gap is δ = 0.1 cm, and the total cross-sectional area of ​​the electromagnet is S = 2 cm2. Estimate the pull force of the relay.

Inductance B is determined by successive approximations using the equation I ∙ ω = Hс ∙ lс + Hδ ∙ 2 ∙ δ.

Let n. c. Hc ∙ lc is 15% I ∙ ω, i.e. 18 Av.

Then I ∙ ω-Hс ∙ lс = Hδ ∙ 2 ∙ δ; 120-18 = Hδ ∙ 0.2; Hδ = 102 / 0.2 = 510 A / cm = 51000 A / m.

Hence we find induction B:

Hδ = 8 ∙ 10 ^ 5 V; B = Hδ / (8 ∙ 10 ^ 5) = 51000 / (8 ∙ 10 ^ 5) = 0.0637 T.

After substituting the value B in the formula F = 40550 ∙ B ^ 2 ∙ S, we get:

F = 40550 ∙ 0.0637 ^ 2 ∙ 0.0002 = 0.0326 kg.

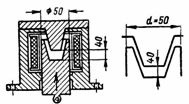
5. The DC brake solenoid (Fig. 5) has a piston armature with a tapered stop. The distance between the armature and the core is 4 cm. The working diameter (cores with a circular contact area) d = 50 mm. The armature is pulled into the coil with a force of 50 kg. The length of the middle line of force lav = 40 cm. Determine n. pp. and the coil current if there are 3000 turns.

Rice. 5. DC brake solenoid

The area of ​​the working section of the electromagnet is equal to the area of ​​a circle with a diameter d = 5 cm:

S = (π ∙ d ^ 2) / 4 = 3.14 / 4 ∙ 25 = 19.6 cm2.

The induction B required to create a force F = 50 kg is found from the equation F = 40550 ∙ B ^ 2 ∙ S,

where B = √ (F / (40550 ∙ S)) = √ (50 / (40550 ∙ 0.00196)) = 0.795 T.

Magnetizing force I ∙ ω = Hс ∙ lс + Hδ ∙ δ.

We determine the magnetizing strength for steel Hc ∙ lc in a simplified way, based on the fact that it is 15% I ∙ ω:

I ∙ ω = 0.15 ∙ I ∙ ω + Hδ ∙ δ; 0.85 ∙ I ∙ ω = Hδ ∙ δ; 0.85 ∙ I ∙ ω = 8 ∙ 10 ^ 5 ∙ B ∙ δ; I ∙ ω = (8 ∙ 10 ^ 5 ∙ 0.795 ∙ 0.04) / 0.85 = 30,000 Av.

Magnetizing current I = (I ∙ ω) / ω = 30000/3000 = 10 A.