Magnetic field strength. Magnetizing force

There is always an electric current around a wire or coil magnetic field… The magnetic field of a permanent magnet is caused by the movement of electrons in their orbits in the atom.

A magnetic field is characterized by its strength. The strength H of the magnetic field is similar to the mechanical strength. It is a vector quantity, that is, it has magnitude and direction.

The magnetic field, that is, the space around the magnet, can be represented as filled with magnetic lines, which are considered to exit from the north pole of the magnet and enter the south pole (Fig. 1). The tangents to the magnetic line indicate the direction of the magnetic field strength.

The magnetic field is stronger where the magnetic lines are denser (at the poles of a magnet or inside a current-carrying coil).

The greater the current I and the number of turns ω of the coil, the greater the magnetic field near the wire (or inside the coil).

The strength of the magnetic field H at any point in space is greater the greater the product ∙ ω and the shorter the length of the magnetic line:

H = (I ∙ ω) / l.

It follows from the equation that the unit for measuring the strength of the magnetic field is the ampere per meter (A / m).

For each magnetic line in a given uniform field, the products H1 ∙ l1 = H2 ∙ l2 = … = H ∙ l = I ∙ ω are equal (Fig. 1).

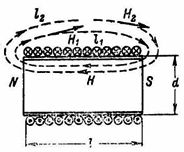
Rice. 1.

The product H ∙ l in magnetic circuits is similar to the voltage in electric circuits and is called the magnetic voltage, and taken along the entire length of the magnetic induction line is called the magnetizing force (ns) Fm: Fm = H ∙ l = I ∙ ω.

The magnetizing force Fm is measured in amperes, but in technical practice, instead of the name ampere, the name ampere-turn is used, which emphasizes that Fm is proportional to the current and the number of turns.

For a cylindrical coil without a core, the length of which is much greater than its diameter (l≫d), the magnetic field inside the coil can be considered uniform, i.e. with the same magnetic field strength H in the entire internal space of the coil (Fig. 1). Since the magnetic field outside such a coil is much weaker than inside it, the external magnetic field can be neglected and in the calculation it is assumed that n. c coil is equal to the product of the field strength inside the coil times the length of the coil.

The polarity of the magnetic field of the wire and current coil is determined by the gimbal rule. If the forward movement of the gimbal coincides with the direction of the current, then the direction of rotation of the gimbal handle will indicate the direction of the magnetic lines.

Examples of

1. A current of 3 A flows through a coil of 2000 turns. What is n. v. coils?

Fm = I ∙ ω = 3 ∙ 2000 = 6000 A. The magnetizing strength of the coil is 6000 ampere-turns.

2. A coil of 2500 turns should have n. p. 10000 A. What current must flow through it?

I = Fm / ω = (I ∙ ω) / ω = 10000/2500 = 4 A.

3.A current I = 2 A flows through the coil. How many turns must there be in the coil to provide n. village 8000 A?

ω = Fm / I = (I ∙ ω) / I = 8000/2 = 4000 turns.

4. Inside a coil 10 cm long with 100 turns, it is necessary to ensure the strength of the magnetic field H = 4000 A / m. How much current should the coil carry?

The magnetizing force of the coil is Fm = H ∙ l = I ∙ ω. Therefore, 4000 A / m ∙ 0.1 m = I ∙ 100; I = 400/100 = 4 A.

5. The diameter of the coil (solenoid) is D = 20 mm, and its length is l = 10 cm. The coil is wound from a copper wire with a diameter of d = 0.4 mm. What is the magnetic field strength inside the coil if it is switched on at 4.5V?

The number of turns without taking into account the thickness of the insulation ω = l∶d = 100∶0.4 = 250 turns.

Loop length π ∙ d = 3.14 ∙ 0.02 m = 0.0628 m.

Coil length l1 = 250 ∙ 0.0628 m = 15.7 m.

The active resistance of the coil r = ρ ∙ l1 / S = 0.0175 ∙ (4 ∙ 15.7) / (3.14 ∙ 0.16) = 2.2 Ohm.

Current I = U / r = 4.5 / 2.2 = 2.045 A ≈2 A.

The strength of the magnetic field inside the coil H = (I ∙ ω) / l = (2 ∙ 250) / 0.1 = 5000 A / m.

6. Determine the strength of the magnetic field at a distance of 1, 2, 5 cm from the straight wire through which the current I = 100 A flows.

Let's use the formula H ∙ l = I ∙ ω.

For a straight wire ω = 1 and l = 2 ∙ π ∙ r,

whence H = I / (2 ∙ π ∙ r).

H1 = 100 / (2 ∙ 3.14 ∙ 0.01) = 1590 A / m; H2 = 795 A/m; H3 = 318 A/m.