Calculation of the power of three-phase current

In the article, to simplify the notation, the linear values ​​of voltage, current and power of a three-phase system will be given without subscripts, i.e. U, I and P.

The power of a three-phase current is equal to three times the power of a single phase.

When star connected PY = 3 Uph Iphcosfi = 3 Uph Icosfie.

When connected by a triangle P = 3 Uph Iphcosfi= 3 U Iphcosfie.

In practice, a formula is used in which current and voltage mean linear quantities for both star and delta connections. In the first equation we substitute Uph = U / 1.73, and in the second Iph = I / 1.73 we get the general formula P =1, 73 U Icosfie.

Examples of

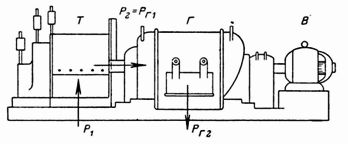
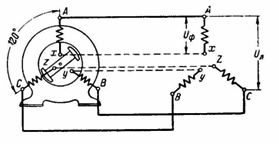
1. What power P1 is received from the network by the three-phase induction motor shown in fig. 1 and 2 when connected in star and delta if the line voltage U = 380 V and the line current I = 20 A at cosfie=0.7·

The voltmeter and ammeter show linear values, average values.

Rice. 1.

Rice. 2.

Engine power according to the general formula will be:

P1 = 1.73 U Icosfie=1.73·380 20 0.7 = 9203 W = 9.2 kW.

If we calculate the power by the phase values ​​of current and voltage, then when connected to a star, the phase current is If = I = 20 A, and the phase voltage Uf = U / 1.73 = 380 / 1.73,

hence the power

P1 = 3 Uph Iphcosfie= 3 U / 1.73 Icosfie=31.7380/1.73·20·0.7;

P1 = 3·380 / 1.73 20 0.7 = 9225 W = 9.2 kW.

When connected in a triangle, the phase voltage Uph = U and the phase current Iph = I /1.73=20/1, 73; thus,

P1 = 3 Uph Iphcosfie= 3 U I /1.73·cosfie;

P1 = 3·380 20 / 1.73 0.7 = 9225 W = 9.2 kW.

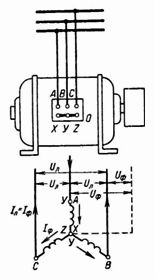
2. The lamps are connected to the four-wire three-phase current network between the line and neutral wires, and the motor D is connected to the three line wires, as shown in fig. 3.

Rice. 3.

Each phase includes 100 lamps of 40 W each and 10 motors with a power of 5 kW. What active and total power must the generator G give at sinfi = 0.8 What are the phase, line and neutral currents of the generator at a voltage U = 380 V

The total power of the lamps is Pl = 3 100 40 W = 12000 W = 12 kW.

The lamps are under phase voltage Uf = U /1, 73 = 380 / 1.73 = 220 V.

The total power of three-phase motors Pd = 10 5 kW = 50 kW.

The active power delivered by the generator, PG, and received by the consumer P1 is equal, if we ignore the power loss in the transmission wires:

P1 = PG = Pl + Pd = 12 + 50 = 62 kW.

Apparent generator power S = PG /cosfie = 62 / 0.8 = 77.5 kVA.

In this example, all phases are equally loaded and therefore the current in the neutral wire at any instant is zero.

The phase current of the stator winding of the generator is equal to the line current (Iph = I) and its value can be obtained by the formula for the power of the three-phase current:

I = P / (1.73Ucosfie) = 62000 / (1.73 380 0.8) = 117.8 A.

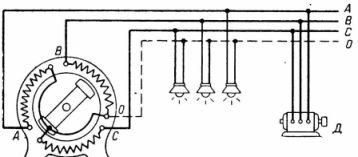
3. In fig.4 shows that a 500 W plate is connected to phase B and the neutral wire, and a 60 W lamp is connected to phase C and the neutral wire. Three phases ABC are connected to a 2 kW motor at cosfie= 0.7 and an electric stove of 3 kW.

What is the total active and apparent power of consumers What currents pass through individual phases at a network voltage U = 380 V

Rice. 4.

Active power of consumers P = 500 + 60 + 2000 + 3000 = 5560 W = 5.56 kW.

Full motor power S = P /cosfie = 2000 / 0.7 = 2857 VA.

The total apparent power of the consumers will be: Stot = 500 + 60 + 2857 + 3000 = 6417 VA = 6.417 kVA.

Electric stove current Ip = Pp / Uf = Pp / (U1, 73) = 500/220 = 2.27 A.

Lamp current Il = Pl / Ul = 60/220 = 0.27 A.

The current of the electric stove is determined by the power formula for three-phase current at cosfie= 1 (active resistance):

P =1, 73 U Icosfie=1, 73 * U * I;

I = P / (1.73 U) = 3000 / (1.73·380) = 4.56 A.

Motor current ID = P / (1.73Ucosfie)=2000/(1.73380 0.7) = 4.34A.

The phase A conductor carries current from the motor and the electric stove:

IA = ID + I = 4.34 + 4.56 = 8.9 A.

In phase B, the current flows from the motor, the hotplate and the electric stove:

IB = ID + Ip + I = 4.34 + 2.27 + 4.56 = 11.17 A.

In phase C current flows from the motor, the lamp and the electric stove:

IC = ID + Il + I = 4.34 + 0.27 + 4.56 = 9.17 A.

RMS currents are given everywhere.

In fig. 4 shows the protective grounding 3 of the electrical installation. The neutral wire is grounded tightly to the power substation and the consumer. All parts of the installations that can be touched by a person are connected to the neutral wire and are thus grounded.

If one of the phases is accidentally earthed, for example C, a single-phase short circuit occurs and a fuse or circuit breaker for that phase disconnects it from the power source. If a person standing on the ground touches an uninsulated wire of phases A and B, it will be under phase voltage only. With an ungrounded neutral, phase C will not be disconnected and the face will be energized with respect to phases A and B.

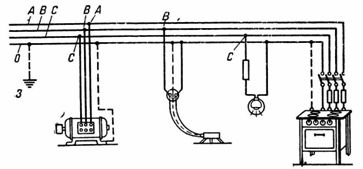
4. What power is supplied to the motor will be shown by a three-phase wattmeter connected to a three-phase network with a line voltage U = 380 V at a line current I = 10 A and cosfie= 0.7 · K. p. D. On the motor = 0.8 What is the power of the motor on the shaft (Fig. 5) ·

Rice. 5.

The wattmeter will show the power supplied to motor P1 ie. the net power P2 plus the power loss in the motor:

P1 =1.73U Icosfie=1.73·380 10 0.7 = 4.6 kW.

Net power minus coil and steel losses and mechanical losses in the bearings

P2 = 4.6 0.8 = 3.68 kW.

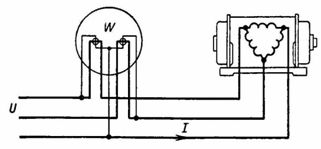
5. A three-phase generator supplies current I = 50 A at voltage U = 400 V and cosfie= 0.7. What mechanical power in horsepower is required to turn the generator when the efficiency of the generator is 0.8 (Fig. 6)

Rice. 6.

Active electrical power of the generator given to the electric motor, PG2 = (3) U Icosfie= 1.73 400 50 0.7 = 24 220 W = 24.22 kW.

The mechanical power supplied to the generator, PG1, covers the active power of PG2 and its losses: PG1 = PG2 / G = 24.22 / 0.8·30.3 kW.

This mechanical power, expressed in horsepower, is:

PG1 = 30.3 * 1.36 * 41.2 liters. with

In fig. 6 shows that the mechanical power PG1 is supplied to the generator. The generator converts it into electric, which is equal to

This power, active and equal to PG2 = 1.73 U Icosfie, is transmitted by wires to an electric motor, where it is converted into mechanical power.In addition, the generator sends reactive power Q to the electric motor, which magnetizes the motor, but is not consumed in it, but returned to the generator.

It is equal to Q = 1.73 · U · I · sinfi and is not converted into either thermal or mechanical power. Apparent power S = Pcosfie, as we saw earlier, only determines the degree of utilization of the materials consumed in the manufacture of the machine.]

6. A three-phase generator operates at voltage U = 5000 V and current I = 200 A at cosfie= 0.8. What is its efficiency if the power given by the engine turning the generator is 2000 hp? with

Engine power applied to the generator shaft (if there are no intermediate gears),

PG1 = 2000 0.736 = 1473 kW.

The power developed by a three-phase generator is

PG2 = (3) U Icosfie= 1.73 5000 200 0.8 = 1384000 W = 1384 kW.

Generator efficiency PG2 / PG1 = 1384/1472 = 0.94 = 94%.

7. What current flows through the winding of a three-phase transformer at a power of 100 kVA and voltage U = 22000 V at cosfie=1

Apparent power of the transformer S = 1.73 U I = 1.73 22000 I.

Therefore, the current I = S / (1.73 U) = (100 1000) / (1.73 22000) = 2.63 A .;

8. What is the current consumed by a three-phase induction motor with a shaft power of 40 liters? with a voltage of 380 V, if its cosfie = 0.8, and the efficiency = 0.9

Motor power on the shaft, that is, useful, P2 = 40736 = 29440 W.

The power supplied to the motor, i.e. the power received from the mains,

P1 = 29440 / 0.9 = 32711W.

Motor current I = P1 / (1.73 U Icosfie)=32711/(1.73·380 0.8) = 62 A.

9. A three-phase induction motor has the following data on the panel: P = 15 hp. with .; U = 380/220 V; cosfie= 0.8 connection — star. The values ​​indicated on the plate are called nominal.

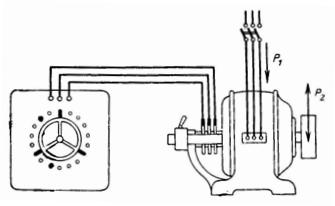
Rice. 7.

What are the active, apparent and reactive forces of the engine? What are the currents: full, active and reactive (Fig. 7)?

The mechanical power of the motor (mains) is:

P2 = 15 0.736 = 11.04 kW.

The supplied power P1 to the motor is greater than the useful power by the amount of losses in the motor:

P1 = 11.04 / 0.85 13 kW.

Apparent power S = P1 /cosfie = 13 / 0.8 = 16.25 kVA;

Q = S sinfi = 16.25 0.6 = 9.75 kvar (see power triangle).

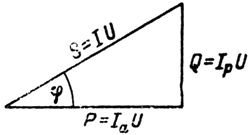
The current in the connecting wires, i.e. linear, is equal to: I = P1 / (1.73 Ucosfie) = S / (1.73 U) = 16250 / (1.731.7380) = 24.7 A.

Active current Ia = Icosfie= 24.7 0.8 = 19.76 A.

Reactive (magnetizing) current Ip = I sinfi = 24.7 0.6 = 14.82 A.

ten. Determine the current in the winding of a three-phase electric motor if it is delta connected and the net power of the motor P2 = 5.8 liters. with efficiency = 90%, power factor cosfie = 0.8 and mains voltage 380 V.

Net engine power P2 = 5.8 hp. sec., or 4.26 kW. Power to the motor

P1 = 4.26 / 0.9 = 4.74 kW. I = P1 / (1.73 Ucosfie)=(4.74·1000)/(1.73·380 0.8) = 9.02 A.

When connected in a delta, the current in the motor phase winding will be less than the current in the supply wires: If = I / 1.73 = 9.02 / 1.73 = 5.2 A.

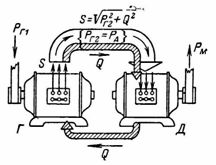
11. A DC generator for an electrolysis plant, designed for voltage U = 6 V and current I = 3000 A, in connection with a three-phase asynchronous motor forms a motor generator. The efficiency of the generator is G = 70%, the efficiency of the motor is D = 90%, and the power factor ecosfie= 0.8. Determine the power of the shaft motor and the power supply to it (Fig. 8 and 6).

Rice. eight.

Net power of generator PG2 = UG · IG = 61.73000 = 18000 W.

The power supplied to the generator is equal to the shaft power P2 of the drive induction motor, which is equal to the sum of PG2 and the power losses in the generator, i.e. PG1 = 18000 / 0.7 = 25714 W.

The active power of the motor supplied to it from the AC mains,

P1 = 25714 / 0.9 = 28571 W = 28.67 kW.

12. A steam turbine with efficiency · T = 30% rotates the generator with efficiency = 92% and cosfie= 0.9. What input power (hp and kcal / s) should the turbine have in order for the generator to provide a current of 2000 A at a voltage of U = 6000 V (Before starting the calculation, see Fig. 6 and 9.)

Rice. nine.

The alternator power supplied to the consumer is

PG2 = 1.73·U Icosfie= 1.73 6000 2000 0.9 = 18684 kW.

The supplied power of the generator is equal to the power P2 of the turbine shaft:

PG1 = 18684 / 0.92 = 20308 kW.

Power is supplied to the turbine by steam

P1 = 20308 / 0.3 = 67693 kW,

or P1 = 67693 1.36 = 92062 hp. with

The supplied power of the turbine in kcal / s is determined by the formula Q = 0.24 · P · t;

Q t = 0.24 P = 0.24 67693 = 16246 kcal / sec.

13. Determine the cross-section of the 22 m long wire through which the current flows to the 5-liter three-phase motor. c. voltage 220 V when connecting the stator winding in a triangle. cosfie= 0.8; · = 0.85. Permissible voltage drop in the wires U = 5%.

Power input to the motor at net power P2

P1 = (5 0.736) / 0.85 = 4.43 kW.

The current I = P1 / (U 1.73cosfie) = 4430 / (220 1.73 0.8) = 14.57 A.

In a three-phase line, the currents add up geometrically, therefore the voltage drop in the conductor should be taken as U:1.73, not U:2 as for single-phase current. Then the resistance of the wire:

r = (U: 1.73) / I = (11: 1.73) / 14.57 = 0.436 Ohm,

where U is in volts.

S = 1/57 22 / 0.436 = 0.886 mm2

The cross-section of the wires in a three-phase circuit is smaller than in a single-phase circuit.

14. Determine and compare the cross-sections of conductors for directly alternating single-phase and three-phase currents. 210 lamps of 60 W each for a voltage of 220 V are connected to the network, located at a distance of 200 m from the source of current. Allowable voltage drop 2%.

a) In direct and single-phase alternating currents, that is, when there are two conductors, the cross-sections will be the same, because under lighting load cosfie= 1 and the transmitted power

P = 210 60 = 12600 W,

and the current I = P / U = 12600/220 = 57.3 A.

Permissible voltage drop U = 220 2/100 = 4.4 V.

The resistance of the two wires is r = U / I 4.4 / 57.3 = 0.0768 Ohm.

Cross section of the wire

S1 = 1/57 * (200 * 2) / 0.0768 = 91.4 mm2.

For energy transfer, a total cross-section of 2 S1 = 2 91.4 = 182.8 mm2 with a wire length of 200 m is required.

b) With three-phase current, the lamps can be connected in a triangle, 70 lamps per side.

At cosfie= 1 power transmitted through the wires P = 1.73 · Ul · I.

I = P / (U 1.73) = 12600 / (220 1.73) = 33.1 A.

The permissible voltage drop in one conductor of a three-phase network is not U · 2 (as in a single-phase network), but U · 1.73. The resistance of one wire in a three-phase network will be:

r = (U: 1.73) / I = (4.4: 1.73) / 33.1 = 0.0769 Ohm;

S3ph = 1/57200 / 0.0769 = 45.7 mm2.

The total cross-section of the wires for a transmission power of 12.6 kW in a three-phase network with a delta connection is less than in a single-phase one: 3 · S3ph = 137.1 mm2.

c) When connected in a star, a network voltage U = 380 V is required so that the phase voltage of the lamps is 220 V, i.e. so that the lamps are switched on between the neutral wire and each linear.

The current in the wires will be: I = P / (U: 1.73) = 12600 / (380: 1.73) = 19.15 A.

Wire resistance r = (U: 1.73) / I = (4.4: 1.73) / 19.15 = 0.1325 Ohm;

S3sv = 1/57200 / 0.1325 = 26.15 mm2.

The total cross-section when star-connected is the smallest that can be achieved by increasing the voltage to transmit a given power: 3 · S3sv = 3 · 25.15 = 75.45 mm2.

See also: Calculation of phase and line values ​​of three-phase current