Determination of engine power during repetitive transient operation

The mode of operation of the electric drive, in which the periods of operation are of such duration, and so alternate with pauses of a certain duration, that the temperature of all the devices that make up the electric drive does not reach a stable value, neither during each period of work, nor during each break, interrupt is called.

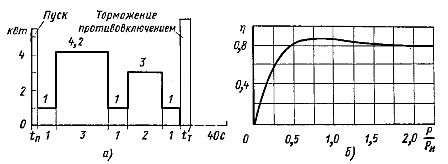
The periodic loading regime corresponds to graphs similar to those shown in Fig. 1. The overheating of the electric motor varies along the dashed line of a saw consisting of alternating segments of heating and cooling curves. Intermittent load mode is typical of most machine tool drives.

Rice. 1. Intermittent load schedule

The power of an electric motor operating in periodic mode is most conveniently determined by the formula for average losses, which can be written as

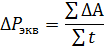
where ΔA is the energy loss at each load value, including the starting and stopping processes.

When the electric motor is not working, the cooling conditions deteriorate significantly. This is taken into account by introducing experimental coefficients β0 <1. The pause time t0 is multiplied by the coefficient β0, as a result of which the denominator of the formula decreases, and the equivalent losses ΔREKV increase and, accordingly, the nominal power of the electric motor increases.

For asynchronous protected motors of the A series with a synchronous speed of 1500 rpm and a power of 1-100 kW, the β0 coefficient is 0.50-0.17, and for blow-down motors β0 = 0.45-0.3 (with an increase in Пн , coefficient β0 decreases). For closed motors, β0 is close to unity (0.93-0.98). This is because the ventilation efficiency of closed engines is low.

When starting and stopping, the average speed of the electric motor is lower than the nominal one, as a result of which the cooling of the electric motor also deteriorates, which is characterized by the coefficient

When determining the coefficient β1, it is conditionally assumed that the change in the rotation frequency occurs according to a linear law and that the coefficient β1 linearly depends on it.

Knowing the coefficients β0 and β1, we get

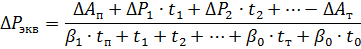
where ΔР1, ΔР2, — power losses at different loads, kW; t1 t2 — action time of these loads, s; tn, tT, t0 — start, delay and pause time, s; ΔАп ΔАТ — energy losses in the engine during starting and stopping, kJ.

As stated above, each motor must be selected for heating and overload conditions. In order to apply the method of average losses, it is necessary to set up a certain electric motor in advance, which in this case is also recommended to be selected according to the overload conditions.The equivalent power formula can be used for a rough calculation in cases where starting and stopping are rare and do not significantly affect the heating of the electric motor.

In mechanical engineering, for operation in intermittent load mode, electric motors designed to operate with a continuous load are used. The electrical industry also produces motors specially designed to handle intermittent loads, which are widely used in lifting and transport structures. Such electric motors are selected taking into account the relative duration of inclusion:

where tp is the engine running time; t0 — pause duration.

An example of choosing a motor by power in multiple short-term operation mode.

Determine the power of the electric motor at n0 — 1500 rpm; the motor operates according to the load schedule shown in fig. 2, a. Electric motor shaft power at machine idle Pxx = 1 kW. Reduced moment of inertia of the machine Jc = 0.045 kg-m2.

Answer:

1. Preselect the electric motor according to the overload conditions, such as λ = 1.6:

According to the catalog, we choose an electric motor with the protected version of the nearest high power (2.8 kW), in which mon = 1420 rpm;

For this engine λ = 0.85 • 2 = 1.7. In this way, the motor is selected with a certain overload limit.

The dependence η = f (P / Pн) of this engine is shown in fig. 2, b.

Rice. 2. Dependencies N = f (t) and η = f (P / Pн)

2. According to the formula

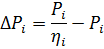
we detect losses at powers 1; 3; 4.2 kW (on schedule). The losses are respectively 0.35; 0.65 and 1 kW. We find losses at Pn = 2.8 kW, which are ΔPn = 0.57 kW.

3. Determine the start time and stop time by opposition:

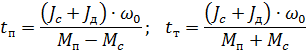
where:

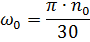
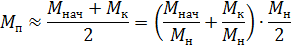
We get tn = 0.30 s; tt = 0.21 s.

4. Determine the starting and stopping losses:

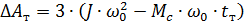
We get ΔAp = 1.8 kJ and ΔAt = 3.8 kJ.

5. Find the equivalent losses in the loop:

where

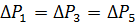
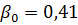
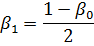
We get ΔREKV = 0.44 kW. Since ΔPn = 0.57, then ΔREKV <ΔPn and therefore the motor is correctly selected.