Heating and cooling of electric motors

Correct determination of the power of electric motors for various metal cutting machines, mechanisms and machines is of great importance. With insufficient power, it is impossible to fully use the production capabilities of the machine, to carry out the planned technological process. If the power is insufficient, the electric motor will fail prematurely.

Overestimating the power of the electric motor leads to its systematic undercharging and, as a result, incomplete use of the motor, its operation with low efficiency and a small power factor (for asynchronous motors). Also, when engine power is overrated, capital and operating costs increase.

The power required to operate the machine, and therefore the power developed by the electric motor, changes during machine operation. The load on an electric motor can be characterized by the load graph (Fig. 1), which is the dependence of the power from the motor shaft, its torque or current on time.After finishing processing the workpiece, the machine is stopped, the workpiece is measured, and the workpiece is replaced. The loading schedule is then repeated again (when processing parts of the same type).

To ensure normal operation under such a variable load, the electric motor must develop the highest required power during processing and not overheat during continuous operation in accordance with this load schedule. The permissible overload of electric motors is determined by their electrical properties.

Rice. 1. Load the schedule when machining the same type of parts

When the engine is running, energy (and power) lossescausing it to heat up. Part of the energy consumed by the electric motor is spent on heating its windings, on heating the magnetic circuit of hysteresis and eddy currents carrying friction and air friction. The heat losses of the windings, proportional to the square of the current, are called variable (ΔРtrans)... The remaining losses in the motor depend a little on its load and are conventionally called constants (ΔРpos).

The permissible heating of an electric motor is determined by the least heat-resistant materials of its construction. This material is the insulation of its coil.

The following are used to insulate electrical machines:

• cotton and silk fabrics, yarns, paper and fibrous organic materials that are not impregnated with insulating compounds (heat resistance class U);

• the same materials, impregnated (class A);

• synthetic organic films (class E);

• materials from asbestos, mica, fiberglass with organic binders (class B);

• the same, but with synthetic binders and impregnating agents (class F);

• the same materials, but with silicon binders and impregnating agents (class H);

• mica, ceramics, glass, quartz without binders or with inorganic binders (class C).

Insulation classes U, A, E, B, F, H respectively allow maximum temperatures of 90, 105, 120, 130, 155, 180 ° C. The limiting temperature of class C exceeds 180 ° C and is limited by the properties of the materials used .

With the same load on the electric motor, its heating will be uneven at different ambient temperatures. The design temperature t0 of the environment is 40 ° C. At this temperature, the nominal power values ​​of the electric motors are determined. The increase in the temperature of the electric motor above the ambient temperature is called overheating:

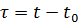
The use of synthetic insulation is expanding. In particular, silicon silicon insulations ensure high reliability of electrical machines when operating in tropical conditions.

The heat generated in different parts of the engine affects the heating of the insulation to different degrees. In addition, heat exchange takes place between the individual parts of the electric motor, the nature of which changes depending on the load conditions.

The different heating of the individual parts of the electric motor and the transfer of heat between them complicates the analytical study of the process. Therefore, for simplicity, it is conditionally assumed that the electric motor is a thermally homogeneous and infinitely heat-conducting body. It is generally believed that the heat released by an electric motor to the environment is proportional to superheat.In this case, thermal radiation is neglected because the absolute heating temperatures of the engines are low. Consider the heating process of the electric motor under the given assumptions.

When working in the electric motor, the heat dq is released during the time dt. Part of this heat dq1 is absorbed by the mass of the electric motor, as a result of which the temperature t and overheating τ of the motor increase. The remaining heat dq2 is released from the engine to the environment. Thus the equality can be written

As the engine temperature increases, the heat dq2 increases. At a certain value of overheating, as much heat will be given to the environment as is released in the electric motor; then dq = dq2 and dq1 = 0. The temperature of the electric motor stops increasing and the overheating reaches a stationary value of τу.

Under the above assumptions, the equation can be written as follows:

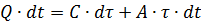
where Q is the thermal power due to losses in the electric motor, J / s; A — heat transfer from the engine, i.e. the amount of heat released by the engine into the environment per unit time at a temperature difference between the engine and the environment of 1oC, J / s-deg; C is the thermal capacity of the motor, i.e. the amount of heat required to increase the temperature of the engine by 1 ° C, J / deg.

Separating the variables in the equation, we have

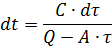
We integrate the left side of the equality in the range from zero to some current value of time t and the right side in the range from the initial overheating τ0 of the electric motor to the current value of overheating τ:

Solving the equation for τ, we obtain an equation for heating an electric motor:

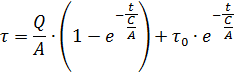
Let us denote C / A = T and determine the dimension of this ratio:

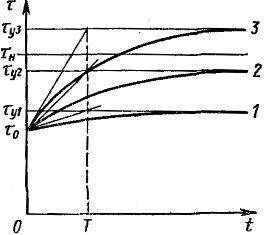
Rice. 2. Curves characterizing the heating of the electric motor

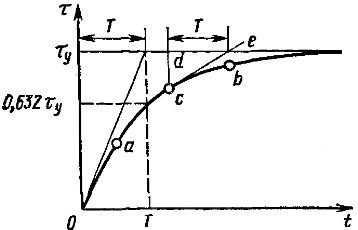
Rice. 3. Determination of the heating time constant

It is called the quantity T, which has the dimension of time heating time constant electric motor. In accordance with this notation, the heating equation can be rewritten as

As you can see from the equation, when we get — steady-state superheat value.

When the load on the electric motor changes, the amount of losses changes and therefore the value of Q. This leads to a change in the value of τу.

In fig. 2 shows the heating curves 1, 2, 3 corresponding to the last equation for different load values. When τу exceeds the value of the permissible overheating τn, the continuous operation of the electric motor is unacceptable. As follows from the equation and graphs (Fig. 2), the increase in superheat is asymptotic.

When we substitute the value t = 3T into the equation, we get a value of τ that is approximately only 5% less than τy. Thus, during the time t = 3T, the heating process can practically be considered complete.

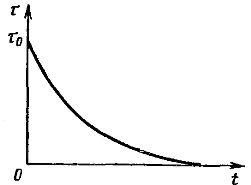
If at any point with the heating curve (Fig. 3) you draw a tangent to the heating curve, then draw a vertical through the same point, then the segment de of the asymptote, closed between the tangent and the vertical, on the scale of the abscissa axis is equal to T. If we take Q = 0 in the equation, we get the motor cooling equation:

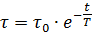
The cooling curve shown in Fig. 4, corresponds to this equation.

The time constant of heating is determined by the size of the electric motor and the form of its protection against environmental influences. For open and protected low-power electric motors, the heating time is 20-30 minutes. For closed high-power electric motors, it reaches 2-3 hours.

As mentioned above, the stated theory of electric motor heating is approximate and based on rough assumptions. Therefore, the heating curve measured experimentally differs significantly from the theoretical one. If, for different points of the experimental heating curve, the construction shown in Fig. 3, it turns out that the values ​​of T increase with increasing time. Therefore, all calculations made according to the equation should be considered approximate. In these calculations it is advisable to use the constant T determined graphically for the starting point of the heating curve. This value of T is the smallest and, when used, provides a certain margin of engine power.

Rice. 4. Engine cooling curve

The experimentally measured cooling curve differs from the theoretical one even more than the heating curve. The cooling time constant corresponding to the engine off is significantly longer than the heating time constant due to reduced heat transfer in the absence of ventilation.