Heating of live parts with continuous current flow

Let's look at the basic conditions for heating and cooling electrical equipment, using the example of a homogeneous conductor that is cooled evenly on all sides.

If a current flows through a conductor at ambient temperature, then the temperature of the conductor gradually rises, since all energy losses during the passage of the current are converted into heat.

The rate of rise in the temperature of the conductor when heated by current depends on the ratio between the amount of heat generated and the intensity of its removal, as well as on the heat absorption capacity of the conductor.

The amount of heat generated in the conductor for the time dt will be:

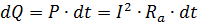
where I is the rms value of the current passing through the conductor, and; Ra is the active resistance of the conductor at alternating current, ohm; P — loss power, converted into heat, wm.Some of this heat goes to heat the wire and raise its temperature, and the remaining heat is removed from the surface of the wire due to heat transfer.

The energy spent on heating the wire is equal to

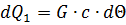
where G is the weight of the current-carrying wire, kg; c is the specific heat capacity of the conductor material, em • sec / kg • grad; Θ — overheating — exceeding the temperature of the conductor relative to the environment:

v and vo — conductor and ambient temperatures, °С.

The energy removed from the surface of the conductor for the time dt due to heat transfer is proportional to the rise in the temperature of the conductor above the ambient temperature:

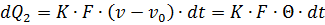
where K is the total coefficient of heat transfer, taking into account all types of heat transfer, Vm / cm2 ° C; F — cooling surface of the conductor, cm2,

The heat balance equation for the time of a transient heat process can be written in the following form:

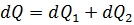
or

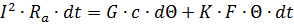
or

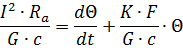
For normal conditions, when the temperature of the conductor varies within small limits, it can be assumed that R, c, K are constant values. In addition, it should be taken into account that before the current was turned on, the conductor was at ambient temperature, i.e. the initial temperature rise of the conductor above the ambient temperature is zero.

The solution of this differential equation for heating the conductor will be

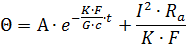
where A is a constant of integration depending on the initial conditions.

At t = 0 Θ = 0, i.e. at the initial moment the heated wire has the ambient temperature.

Then at t = 0 we get

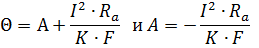
Substituting the value of the integration constant A, we get

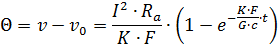
It follows from this equation that the heating of a current-carrying conductor occurs along an exponential curve (Fig. 1). As you can see, with time change, the temperature rise of the wire slows down and the temperature reaches a steady value.

This equation gives the temperature of the conductor at any time t from the beginning of the current flow.

The steady-state superheat value can be obtained if the time t = ∞ is taken into the heating equation

where vu is the stationary temperature of the surface of the conductor; Θу — equilibrium value of the temperature increase of the conductor above the ambient temperature.

Rice. 1. Curves of heating and cooling of electrical equipment: a — change in temperature of a homogeneous conductor with prolonged heating; b — temperature change during cooling

Based on this equation, we can write that

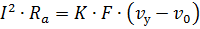
Therefore, it can be seen that when a steady state is reached, all the heat released in the conductor will be transferred to the surrounding space.

Inserting it into the basic heating equation and denoting by T = Gc / KF, we get the same equation in a simpler form:

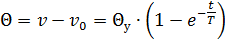
The value T = Gc / KF is called the heating time constant and is the ratio of the body's heat-absorbing ability to its heat-transfer ability. This depends on the size, surface and properties of the wire or body and is independent of time and temperature.

For a given conductor or apparatus, this value characterizes the time to reach a stationary mode of heating and is taken as the scale for measuring time in heating diagrams.

Although it follows from the heating equation that the steady state occurs after an indefinite long time, in practice the time to reach the steady state temperature is taken equal to (3-4) • T, since in this case the heating temperature exceeds 98% of the final its value Θy.

The heating time constant for simple current-carrying structures can be easily calculated, and for apparatus and machines it is determined by thermal tests and subsequent graphical constructions. The time constant of heating is defined as the subtangent OT plotted on the heating curve, and the tangent OT itself to the curve (from the origin) characterizes the rise in temperature of the conductor in the absence of heat transfer.

At high current density and intense heating, the heating constant is calculated using the advanced expression:

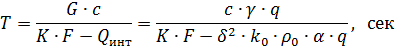
If we assume that the process of heating the conductor takes place without heat transfer to the surrounding space, then the heating equation will have the following form:

and the superheat temperature will increase linearly in proportion to time:

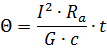
If t = T is substituted in the last equation, then it can be seen that for a period equal to the heating time constant T = Gc / KF, the conductor is heated to the established temperature Θу = I2Ra / KF, if heat transfer does not occur during this time.

The heating constant for electrical equipment varies from a few minutes for buses to several hours for transformers and high power generators.

Table 1 shows the heating time constants for some typical tire sizes.

When the current is turned off, the supply of energy to the wire stops, that is, Pdt = 0, therefore, starting from the moment of turning off the current, the wire will cool.

The basic heating equation for this case is as follows:

Table 1. Heating time constants of copper and aluminum busbars

Tire section, mm *

Heating constants, min

for honey

for aluminum

25×3

7,3

5,8

50×6

14,0

11,0

100×10

20,0

15,8

If the cooling of a conductor or equipment begins with a certain superheat temperature Θy, then the solution of this equation will give the temperature change with time in the following form:

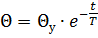
As can be seen from fig. 1b, the cooling curve is the same heating curve but with a downward convexity (toward the abscissa axis).

The heating time constant can also be determined from the cooling curve as the value of the subtangent corresponding to each point on that curve.

The above considered conditions for heating a homogeneous conductor with an electric current to a certain extent are applied to various electrical equipment for a general assessment of the course of heating processes. As for the current-carrying wires of devices, buses and busbars, as well as other similar parts, the conclusions obtained allow us to make the necessary practical calculations.