An electron in an electric field

The movement of an electron in an electric field is one of the most important physical processes for electrical engineering. figure Let's see how this happens in a vacuum. Let us first consider an example of the movement of an electron from the cathode to the anode in a uniform electric field.

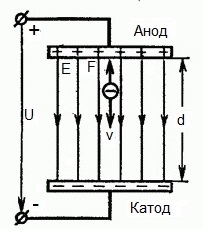
The figure below shows a situation where electron leaves the negative electrode (cathode) with a negligibly small initial velocity (tending to zero) and enters in a uniform electric fieldpresent between two electrodes.

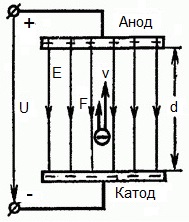
A constant voltage U is applied to the electrodes, and the electric field has a corresponding strength E. The distance between the electrodes is equal to d. In this case, a force F will act on the electron from the side of the field, which is proportional to the charge of the electron and the strength of the field:

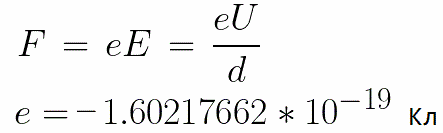
Since the electron has a negative charge, this force will be directed against the field strength vector E. Accordingly, the electron will be accelerated in that direction by the electric field.

The acceleration experienced by the electron is proportional to the magnitude of the force F acting on it and inversely proportional to the electron's mass m.Since the field is uniform, the acceleration for a given picture can be expressed as:

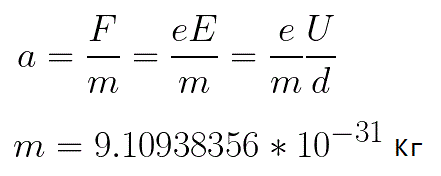
In this formula, the ratio of the electron's charge to its mass is the electron's specific charge, a quantity that is a physical constant:

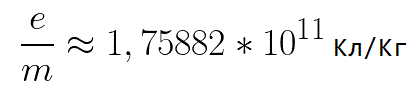
So the electron is in an accelerating electric field because the direction of the initial velocity v0 coincides with the direction of the force F on the side of the field and therefore the electron moves uniformly. If there are no obstacles, it will travel the path d between the electrodes and reach the anode (positive electrode) with a certain speed v. At the moment when the electron reaches the anode, its kinetic energy will be correspondingly equal to:

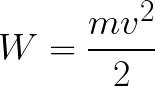
Since along the entire path d the electron is accelerated by the forces of the electric field, it acquires this kinetic energy as a result of the work done by the force acting on the side of the field. This work is equal to:

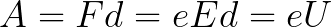
Then the kinetic energy acquired by the electron moving in the field can be found as follows:

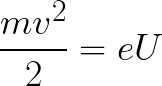
That is, it is nothing more than the work of field forces to accelerate an electron between points with a potential difference U.

In such situations, to express the energy of an electron, it is convenient to use such a unit of measurement as the "electron volt", which is equal to the energy of an electron at a voltage of 1 volt. And since the electron charge is constant, then 1 electrovolt is also a constant value:

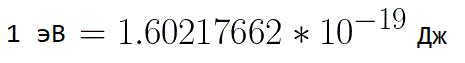
From the previous formula, you can easily determine the speed of the electron at any point on its path when moving in an accelerating electric field, knowing only the potential difference that it passed when accelerating:

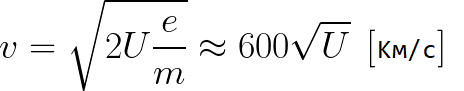
As we can see, the speed of an electron in an accelerating field depends only on the potential difference U between the end point and the start point of its path.

Imagine that the electron starts moving away from the cathode with negligible speed, and the voltage between the cathode and the anode is 400 volts. In this case, at the moment of reaching the anode, its speed will be equal to:

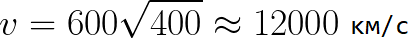
It is also easy to determine the time required for the electron to travel the distance d between the electrodes. With uniformly accelerated motion from rest, the average speed is found to be half of the final speed, then the time of accelerated flight in an electric field will be equal to:

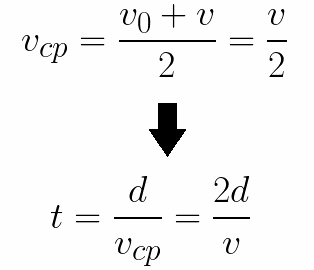
Let us now consider an example when an electron moves in a decelerating uniform electric field. That is, the field is directed as before, but the electron begins to move in the opposite direction — from the anode to the cathode.

Suppose the electron left the anode with some initial velocity v and initially started moving in the direction of the cathode. In this case, the force F acting on the electron from the side of the electric field will be directed against the electric intensity vector E — from the cathode to the anode.

It will start to reduce the initial speed of the electron, that is, the field will slow down the electron. This means that the electron under these conditions will begin to move uniformly and uniformly slowly. The situation is described as follows: "an electron moves in a decelerating electric field."

From the anode, the electron began to move with non-zero kinetic energy, which begins to decrease during the deceleration, since the energy is now expended in overcoming the force acting from the field on the electron.

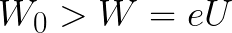
If the initial kinetic energy of the electron as it exits the anode was immediately greater than the energy that must be expended by the field to accelerate the electron in moving from the cathode to the anode (as in the first example), then the electron would travel a distance d and will eventually reach the cathode despite braking.

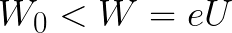
If the initial kinetic energy of the electron is less than this critical value, then the electron will not reach the cathode. At a certain point it will stop, then begin a uniformly accelerated movement back to the anode. As a result, the field will return to it the energy that was spent in the stopping process.

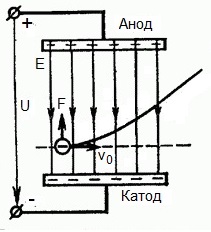
But what if an electron flies with speed v0 in the region of action of an electric field at right angles? Obviously, the force on the side of the field in this region is directed for the electron from the cathode to the anode, that is, against the electric field strength vector E.

This means that now the electron has two components of motion: the first — with a velocity v0 perpendicular to the field, the second — uniformly accelerated under the action of the force from the side of the field directed toward the anode.

It turns out that, having flown into the field of action, the electron moves along a parabolic trajectory. But after flying out of the region of action of the field, the electron will continue its uniform motion by inertia along a straight line trajectory.